parabole i okręgi Kinga: Witam zwracam sie dziś do was z stosunkowo trudnym dla mnie zadaniem. Okrąg przechodzący przez punkt B(5,1) jest styczny do prostej k: x+y−2=0 w punkcie A(1,1). Oblicz pole trójkąta CDS, gdzie S jest środkiem okręgu, zaś C i D są punktami przecięcia się paraboli y=x²−2x z prostą k. Jeśli ktoś jest w stanie to proszę o wytłumaczenie krok po kroku bo jest to dla mnie czarna magia.

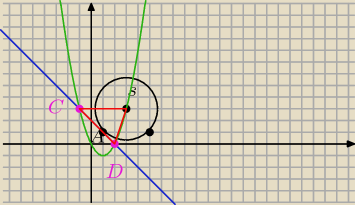
irena_1: Środek okręgu leży na prostej prostopadłej do stycznej, przechodzącej przez punkt styczności. Równanie tej prostej: x−y+k=0 1−1+k=0 k=0 x−y=0 Czyli środek okręgu ma współrzędne typu (a, a). Jest równo odległy od punktów A i B. √(a−1)²+(a−1)²=√(a−5)²+(a−1)² (a−1)²+(a−1)²=(a−5)²+(a−1)² (a−1)²=(a−5)² a²−2a+1=a²−10a+25 8a=24 a=3 S=(3, 3) x+y−2=0 y=x²−2x x+x²−2x−2=0 x²−x−2=0 Δ=1+8=9

	1−3		1+3
x1=		=−1, x2=		=2
	2		2

y₁=3, y₂=0 C=(−1, 3), D=(2, 0) |CS|=√(3+1)²+(3−3)²=√16=4 h− odległość punktu D od odcinka CS (odcinek CS leży na prostej y=3, punkt D leży na osi OX) h=3

	1
P=		*4*3=6
	2

aniabb: