Dane są dwa zdarzenia A i B wykaż nastepującą własność Magda: Wykaż, ze: P(A/B)+P(A/B')=P(A) ⇔ P(A)=0

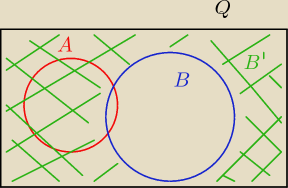
Nienor: A/B' to A−B' P(A−B')=P(A−(1−B))=P(A∩B) (Narysuj zbiorki i sprawdź.) P(A−B)=P(A)−P(A∩B) P(A−B)+P(A−B')=P(A∩B)+P(A)−P(A∩B)=P(A)

Basia: ależ to nieprawda P(A) = P(A/B)+P(A/B') dla dowolnych A,B⊂Ω bo B∪B' = Ω i B∩B' = ∅ czyli spełnione są warunki pozwalające zastosować wzór na prawdopodobieństwo całkowite sprawdź sobie na przykładzie: rzucamy dwa razy monetą A − w drugim rzucie O B − w pierwszym rzucie O B' − w pierwszym rzucie R |Ω| = 4 A/B = {(O,O)}

	1
P(A/B) =
	4

A/B' = {(R,O)}

	1
P(A/B') =
	4

A = {(O,O) (R,O)}

	2
P(A) =		= P(A/B)+P(A/B') i P(A)≠0
	4

Magda: ok ale nie wynika z tego, że to zachodzi wtedy i tylko wtedy, gdy P(A0)=0

Basia: A/B oznacza prawdopodobieństwo warunkowe ( A pod warunkiem B ) nie wpadałabym na to, że to ma być różnica zbiorów

Magda: sorry to do tego pierwszego

Basia: a co to ma być na prawdę ? różnica czy prawdopodobieństwo warunkowe ?

Magda: U nas tak to oznaczyli

Magda: różnica

Basia: to czyli co ?

Magda: przepraszam napisałam "/" zamiast "\" (ma to oznaczać różnicę)

Magda: P(A\B)+P(A\B')=P(A) ⇔ P(A)=0

Basia: jeżeli to jest różnica to masz tak: A−B = A∩B' A−B' = A∩B i są to zdarzenia rozłączne P(A−B)+P(A−B') = P(A∩B')+P(A∩B) = P((A∩B')∪P(A∪B)) = P(A∩(B'∪B)) = P(A∩Ω)=P(A) dla dowolnych A,B⊂Ω a nie tylko dla tych A dla których P(A)=0 Twoje twierdzenie jest fałszywe niezależnie od tego co to P(A/B) i P(A/B') oznacza

Magda: Dzięki