BARDZO PROSZĘ O POMOC : ( malinka: Zadanie 1 Podstawą graniastosłupa prostego jest romb o przekątnych długości d=16 i d=12, a jego objętość równa się V=816. Oblicz pole powierzchni całkowitej. Zadanie 2 Podstawą graniastosłupa prostego jest trójkąt równoramienny o podstawie długości 6 i ramionach długości 5. Odległość między podstawami bryły jest równa 10. Oblicz objętość i pole powierzchni całkowitej. Zadanie 3 Oblicz objętość i pole powierzchni całkowitej graniastosłupa prostego, którego podstawą jest trapez prostokątny o bokach równoległych długości a=8 i b=5 oraz wysokości h=4. Długość wysokości tego graniastosłupa wynosi H=7. Zadanie 4 Oblicz objętość i pole powierzchni całkowitej graniastosłupa prawidłowego sześciokątnego wiedząc, że krawędź podstawy ma długość 4, a wysokość bryły ma długość 12. Zadanie 5 Oblicz objętość i pole powierzchni całkowitej graniastosłupa trójkątnego wiedząc, że wysokość podstawy ma długość 4√3 , a wysokość brył jest równa 20.

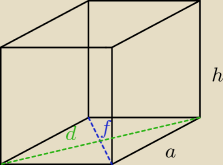
dero2005: d = 16 f = 12 V = 816

	1		1
Pp =		d*f =		*12*16 = 96
	2		2

V = P_p*h = 96*h = 816 → h = 8,5 a = √(^d₂)² + (^f₂)² = √8²+6² = √64+36 = √100 = 10 P_c = 2*P_p + 4*a*h = 2*96 + 4*10*8,5 = 192 + 340 = 532

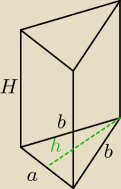
dero2005: zad 2 a= 6 b = 5 H = 10 h = √b² − (^a₂)² = √5² − 3² = √25 − 9 = √16 = 4

	a*h		6*4
Pp =		=		= 12
	2		2

P_c = 2*P_p + 2*b*H + a*H = 2*12 + 2*5*10 + 6*10 = 24 + 100 + 60 = 184 V = P_p*H = 12*10 = 120

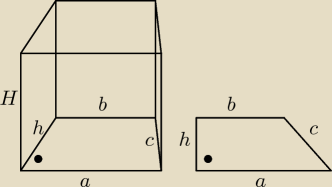
dero2005: zad 3 a = 8 b = 5 h = 4 H = 7 c = √h² + (a−b)² = √4² + 3² = √16 + 9 = √25 = 5

	a+b		8+5
Pp =		*h =		*4 = 26
	2		2

P_c = 2*P_p + H(a+b+c+h) = 2*26 + 7(8 + 5 + 5 + 4) = 52 + 154 = 206 V = P_p*H = 26*7 = 182

dero2005: zad 5 a= 4 H = 12

	3a2√3		3*42√3
Pp =		=		= 24√3
	2		2

P_c = 2*P_p + 6a*H = 2*24√3 + 6*4*12 = 48√3 + 288 = 48(√3 + 6) V = P_p*H = 24√3*12 = 288√3

dero2005: to bylo zad 4 a nie 5

dero2005: zad 5 h_p = 4√3 H = 20

	2
a =		√3*hp = policz
	3

	a2√3
Pp =		= policz
	4

P_c = 2*P_p + 3*a*H = policz V = P_p*H = policz