geometria analityczna Asia: Na prostej x=y znajdź taki punkt C, aby trójkąt był prostokątny. A(1,0), B(5,0)

aniabb: (x−1)²+x²+(5−x)²+x²=16

Anka: a dlaczego tak?

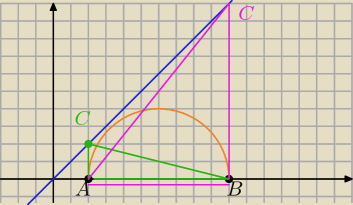
aniabb: z tamtego powinien wyjsc zbiór pusty, bo założyłam że AB najdłuższa a z rys. widać że nie sięga.. więc kąt prosty przy A wtedy C1 (1,1) zielony lub kąt prosty przy B C2(5,5) fioletowy

ola: a to działanie to z jakiegos wzoru?

aniabb: z twierdzenia Pitagorasa

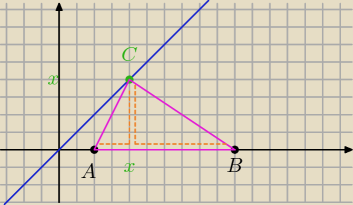
aniabb: AC² +BC²=AB² AC²=(x−1)²+x² BC²=(5−x)²+x² AB²=(5−1)²=4²=16

ola: a czemu jest (x−1)² + x² i z 5 tak samo?

Gustlik: Na prostej x=y znajdź taki punkt C, aby trójkąt był prostokątny. A(1,0), B(5,0) Z wektorów − iloczynem skalarnym: A=(1,0) B=(5,0) C=(x, x) bo leży na prostej y=x 1) kąt prosty w C CA^→=[1−x, 0−x]=[1−x, −x] CB^→=[5−x, 0−x]=[5−x, −x] CA^→*CB^→=0 − warunek prostopadłości. CA^→*CB^→=(1−x)(5−x)+(−x)(−x)=5−x−5x+x²+x²=2x²−6x+5 2x²−6x+5=0 ⇔ Δ=..., x₁=..., x₂=...⇒y₁=x₁=..., y₂=x₂=...⇔ ⇔ C₁=(x₁, x₁) v C₂=(x₂, x₂) A=(1,0) B=(5,0) C=(x, x) bo leży na prostej y=x 2) kąt prosty w A AC^→=[x−1, x−0]=[x−1, x] AB^→=[5−1, 0−0]=[4, 0] AC^→*AB^→=4(x−1)+0*x=4x−4 4x−4=0 ⇔ x=1 ⇔ y=1 ⇔ C=(1, 1) 3) kąt prosty w B BA^→=[1−5, 0−0]=[−4, 0] BC^→=[x−5, x−0]=[x−5, x] BA^→*BC^→=−4(x−5)+0*x=−4x+20 −4x+20=0 −4x=−20 /:(−4) x=5 ⇔ y=5 ⇔ C=(5, 5)