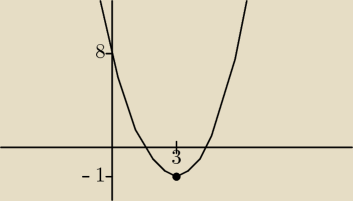
naszkicuj wykres funkcji kwadratowej Dorota: naszkicuj wykres funkcji kwadratowej, o ktorej wiadomo, ze jest malejaca w przedziale (−nieskonczonosci;3), przyjmuje wartosc najmniejsza rowna −1 i przecina os y w punkcie (0,8). zapisz wzor tej funkcji

imię lub nick:

imię lub nick: znasz współrzędne wierzchołaka możesz zapisać wzór tej funkcji w postaci kanonicznej

Dorota: a wzor tej funkcji?

imię lub nick: tyle że jeszcze będziesz musiała wyliczyć współczynnik a

Dorota: a moglbys Ty to zrobic?

imię lub nick: najpierw Ty spróbuj

Dorota: nie wiem... nic nie wymysle

imię lub nick: czego nie wiesz?

Dorota: jak to zrobic

Bogdan: Żeby wymyślić, to trzeba pomyśleć.

imię lub nick: nie będę robił zadania domowego za Ciebie... https://matematykaszkolna.pl/strona/69.html poczytaj troche

Dorota: wspolczynnik a=−3 tak?

imię lub nick: nie wiem nie zapisałaś żadnych obliczeń

Dorota: y=−3(3−3)+16? taki ten wzor?

Dorota: wspolczynnik a: a=x*y a=3*(−1) a=−3

imię lub nick: nie jestem dobrym nauczycielem rezygnuję sorry

Dorota: wzor postaci kanonicznej: y=a(x+p)=q wiec... wspolczynnik a juz obliczony p=−b przez 2a i to jest −3 q=−Δ przez 4a i to jest −16 nie wiem jeszcze czy dobre wstawilam znaki bo (− i + ) zawsze mi sie mylilo

imię lub nick: współczynnik a nie może być ujemny bo ramiona paraboli są skierowane w górę

Dorota: no to wyjdzie to na plusie tak? a=3

imię lub nick: jak zapiszesz wzór w postaci kanonicznej wstw do niego jeden z punktów który należy do wykresy a obliczys a

Dorota: no to nie wiem... poddaje sie do ciorta z tymi zadaniami... nie bede ich robic wcale

imię lub nick: wzór funckji y=a(x−p)+q

Dorota: ...

imię lub nick: Dorota zapisz wszystkie obliczenia z wykorzystaniem tych opcji co masz po lewej stronie łącznie z wzorami funkcji a ja Ci to wszystko spraawdze ok?

Dorota: nie bo i tak zrobie zle....

imię lub nick: f(x)=a(x−3)−1

Dorota: dzieki i przepraszam...

imię lub nick: to ja przepraszam

imię lub nick: jestem słaby z matmy

Dorota: wlasnie ze nie... jestes bardzo dobry i duzo mi pomogles

imię lub nick: ale coś tu jest nie tak bo jak policzyłem a to mi wszyło −3 a tak nie może być. hmmm

Dorota: polcenie przepisalam dobrze...

naomi: wzór funkcji to y=x²−6x+8 czy obliczenia sa potrzene?

Dorota: nie wiem... raczej tak

Dorota: a wykres tej funkcji ktory mi narysowales wyzej jest dobry tak?

naomi: wykres jest dobry, ja go nie rysowalam

Dorota: a sorki to pisal ten chlopak wczesniej... a moglabys mi napisac obliczenia?

Dorota: a popatrzysz pozniej na to zadanko? zapisz wzor funkcji: f(x)=−1/3x do kwadratu−x+6 w postaci iloczynowej

naomi: masz dane punkt(0,8) to sa (x,y) podstawiasz do wzoru ogolnego y=ax²+bx+c i otrzymujesz 8=0+0+c zatem wychodzi c=8 masz nastepnie dany wierzcholek (3,−1) to sa (p,q) czyli (−b/2a , −Δ/4a) to podstawiasz 3=−b/2a −1=−(b²−4ac) / 4a za c wstaw 8 i wychodzi układ dwoch równan z dwiema niewiadomymi wyjdzie a=0 i b=0 to odpada bo to ma byc f. kwadratowa i a=1 i b=−6 to wlasciwy wynik zatem rownanie ma postac y=x²−6x+8.

Dorota: a podaj mi rownanie z ktorego mam obliczyc delte

naomi: obliczasz delte to zwykla funkcja kwadratowa , gdzie a = −1/3 , b= −1 , c=6 Δ=b² − 4ac = 1+8 =9 √Δ =3 x1= −b−√Δ / 2a = 1−3 /2 (−1/3) = 3 x2= −b+√Δ /2a = 1+3 / 2 (−1/3) =−6 i podstawiamy do wzoru y=a(x−x1)(x−x2) czyli y=−1/3 (x−3)(x+6).

Dorota: a moglabys jeszcze to? wykres funkcji g otrzymano przez przesuniecie wykresu funkcji f(x)=1/2 x2 o dwie jednostki w dol. oblicz g(1)

naomi: poszukaj w zeszycie wzorow na przesuniecie to tez proste ale ja moge wzory pomylic i zle policze

naomi: juz wiem g(x)=1/2 x² −2 , to g(1)= 1/2 −2 = −3/2 wszystko

Dorota: zapomnialas o x ze tam przy jednej drugiej jest x wiec go trzeba zamienic na 1... prawda? i wyjdzie ze g(1) bedzie sie rownalo −1 1/2

MATMA TO GÓWNO!: PIERDOLIĆ MATME!