trygonometria Janhuh: muszę rozwiązać 2cos²x<3sinx zamieniłem cos²x na 1−sin²x, podstawiłem sinx za t i teraz zaczyna się zabawa: Wychodzi mi t=¹₂, albo t=−2. Co za tym idzie sinx=¹₂ albo sinx=−2, co jest bzudrą, bo przecież wykres sinusa przyjmuje wartości od −1 do 1. No to biorę sinx=¹₂, zamieniam, wychodzi mi, że x=^π₆+2kπ oraz x=⁵₆π+2kπ. Ale w tym przedziale sin jest zawsze większy od zera. Zrobiłem gdzieś błąd, czy rozwiązaniem jest zbiór pusty?

Tad: ... rozwiązujesz nierówność ... określ więc przedział −

Janhuh: skoro miejsca zerowe wyszły mi x=^π₆+2kπ oraz x=⁵₆π+2kπ, to znaczy, że przedział jest x∊(^π₆+2kπ, x=⁵₆π+2kπ), a w tym przedziale sinx jest większe od 0. Czy może jednak coś skopałem?

Janhuh: pomoże ktoś?

Tad: rozpatrywałeś nierówność 2t²+3t−2>0 dla −1≤t≤1 t=−2 odrzuciłeś z oczywistych powodów zatem nierówność spełniają t>1/2 czyli sinx>1/2 ... i ok

aniabb: ale lepiej jest najpierw odczytać przedział nierówności dla obu t , a dopiero potem ograniczać

Tad: a po cóż dla obu t skoro jedno nie spełnia warunków podstwienia !

aniabb: a jakby wyszło t=2 i t=1/2 to jaki przedział byś wziął?

Tad: tylko t>1/2

Tad: tyle że wtedy t<1/2 z ograniczeniem ale to teoria

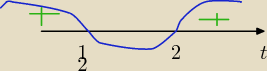
aniabb: dodatnie są dla t <1/2 ... i t>2 który oczywiście odrzucamy

Tad: czy TY rozumiesz co to założenie dla podstawienia

aniabb: czy TY rozumiesz co to rozwiązanie nierówności

Tad: żenada

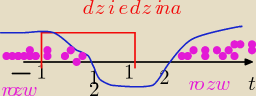
aniabb: tu rozwiązaniem jest przedział <−1 ;1/2 ) a nie (1/2;1>

aniabb: dlatego NIE WOLNO wyrzucać pierwiastków wielomianu przed ustaleniem zbioru rozwiązań niwerówności

aniabb: a dopiero potem się sprawdza z dziedziną

loitzl9006: Ania ma rację, ale moim zdaniem rozwiązaniem będzie jednak przedział (1/2;1>. Gdy podstawimy np. t=0 (czyli x=0) to nierówność nie będzie prawdziwa 2cos²x<3sinx 2(1−sin²x)<3sinx 2−2sin²x<3sinx sinx=t t∊<−1;1> −2t²−3t+2<0 Δ=9−4*(−2)*(2)=9+16=25 √Δ=5

	3−5		−2		1
t1=		=		=
	−4		−4		2

	3+5		8
t2=		=		=−2
	−4		−4

	1
t∊(−∞;−2)∪(		;+∞)
	2

ale t miało należeć do <−1;1>,

	1
więc zostaje z tego t∊(		;1>
	2

	1
zatem t>		i t≤1
	2

	1
sinx>		i sinx≤1
	2

	π		5π
x∊(		+2kπ ;		+2kπ) , k∊C
	6		6

loitzl9006: masz parabolę −2t²−3t+2 (ramiona w dół)

aniabb: ja pokazywałam HIPOTETYCZNY wpływ wyrzucania miejsc zerowych przed ustaleniem rozwiązania..dlatego dałam przykładową 2 zamiast −2 żeby pokazać jak to się zmienia ..wiec nie patrzcie na moje przedziały.. to jest analiza OGÓLNA .. a nie tego konkretnego przykładu

loitzl9006: ok rozumiem Cię