Zadanie bez rozwiązania?
tim: Jak to rozwiązać, zadanie konkursowe z konkursu z obecnej trony (który organizowałem). Zadanie
wziąłem z książki, ale teraz patrzę, że sam nie wiem jak je rozwiązać O.o.
Zadanie:
Wafel do lodów ma kształt stożka o promieniu 2 cm i wysokości 6 cm. Do wafla włożono jedną
porcję lodów. Przyjmij, że porcja lodów ma kształt kuli o średnicy 4 cm. Znajdź odległość
środka lodowej kuli od wierzchołka waflowego stożka.
Odpowiedź:
http://img2.vpx.pl/up/20090514/przechwytywanie.gif
Schemat punktowania:
• Sporządzenie rysunku do zadania i wyróżnienie / zaznaczenie / odpowiednich trójkątów – 1 pkt.
• Dostrzeżenie, że szukana odległość jest równa tworzącej stożka – 1 pkt.
• Wyznaczenie odległości – 1 pkt.
1.Jeżeli uczeń prowadzi obliczenia przyjmując ogólne oznaczenia np. r, R – zadanie oceniamy
zgodnie z kryteriami pod warunkiem, że odpowiedź odnosić się będzie do konkretnych danych z
zadania .
2.Wykonanie błędnego rysunku traktujemy jako zastosowanie błędnej metody ––
/ np. przyjęcie, że połowa kuli została umieszczona w stożku , środek kuli i środek podstawy
stożka pokrywają się, promień kuli jest poprowadzony do wierzchołka trójkąta równoramiennego,
jako przekroju stożka / −
za rozwiązanie całego zadania przyznajemy − 0 pkt.
Bogdan:
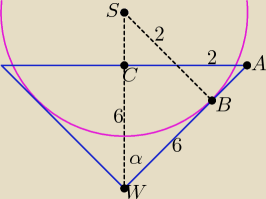
Trójkąty BSW i ACW są przystające, ponieważ w każdym z tych trójkątów kąty mają
miary: α, 90
o − α, 90
o oraz jedna z przyprostokątnych ma długość 2.
|BS| = |AC| = 2
|CW| = |BW| = 6
|SW| = |AW| = ?
Z tw. Pitagorasa: |SW|
2 = |BW|
2 + |BS|
2 ⇒ |SW|
2 = 36 + 4 ⇒ |SW| =
√40 = 2
√10.
 Trójkąty BSW i ACW są przystające, ponieważ w każdym z tych trójkątów kąty mają
miary: α, 90o − α, 90o oraz jedna z przyprostokątnych ma długość 2.
|BS| = |AC| = 2
|CW| = |BW| = 6
|SW| = |AW| = ?
Z tw. Pitagorasa: |SW|2 = |BW|2 + |BS|2 ⇒ |SW|2 = 36 + 4 ⇒ |SW| = √40 = 2√10.
Trójkąty BSW i ACW są przystające, ponieważ w każdym z tych trójkątów kąty mają
miary: α, 90o − α, 90o oraz jedna z przyprostokątnych ma długość 2.
|BS| = |AC| = 2
|CW| = |BW| = 6
|SW| = |AW| = ?
Z tw. Pitagorasa: |SW|2 = |BW|2 + |BS|2 ⇒ |SW|2 = 36 + 4 ⇒ |SW| = √40 = 2√10.
 Dzięki
Dzięki
