wykaż, że funkcja jest malejąca, rosnąca w danych przedziałach. [Z[lemon]]: Wykaż, że funkcja f(x)=2x²−4x jest malejąca w przedziale (−nieskończoność,1) i rosnąca w przedziale (1,+nieskończoność). wiem, jak to zrobić, ale tu chodzi o dowód chyba i w tym problem, że nie jestem dobra w przeprowadzaniu dowodów...

[Z[lemon]]: chyba, że wystarczy narysować wykres i będzie już z wykresu widać ?

PuRXUTM: a nie można tak że znajdujesz p, a=współczynnik przy najwyższej potędze i uzasadniasz słownie

Nienor: Można też policzyć pochodną i zbadać monotoniczność. f'(x)=4x−4 f↗ ⇔ f'(x)>0 f'(x)> ⇔ x>1

[Z[lemon]]: nie miałam pochodnych jeszcze

[Z[lemon]]: PuRXUTM p jako co?

[Z[lemon]]: już wiem xd

[Z[lemon]]: z tym p

[Z[lemon]]: ale dalej nie rozumiem 'a=współczynnik przy najwyższej potędze'

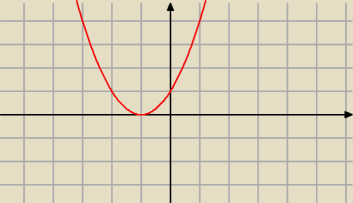
PuRXUTM: jeżeli a− w funkcji kwadratowej >0 to ramiona są " do góry" − wykres funkcji np.x²+2x+1 a =1 bo przed x² jest jedynka 1*x²

Grzybson:

marek_s: Takie zadania wykazuje się na podstawie definicji funkcji malejącej/rosnącej. F. maleje gdy dla x1<x2 f(x1)>f(x2). Zał. x₁<x₂, x₁, x₂ należą (−niesk, 1) Teza: f(x₁)>f(x₂), z czego wynika, że f(x₂)−f(x₁)<0 Podstawiamy 2x₂²−4x₂−(2x₁²−4x₁)<0 trzeba użyć wzoru na różnicę kwadratów i wyjdzie 2(x₂−x₁)(x₂+x₁−2)<0 Z zał. x₂>x₁, więc X₂−x₁ zawsze>0 x₂ i x₁ są<1, więc ich suma zawsze <2, stąd x₂+x₁−2 zawsze<0. Iloczyn "−"*"+" daje "−", więc teza jest prawdziwa.

chichi: to zostało udowodnione dla funkcji kwadratowej w zależności od znaku współczynnika kwadratowego, to samo w przypadku funkcji liniowej (bardzo dobrze znanych funkcji) i korzysta się z tych faktów, bez dowodzenia ich. Ignoranckie jest również Twoje stwierdzenie, że należy dowodzić to w ten sposób, bo polecenie nie wymaga, aby robić to z definicji