Przyśpieszenie styczne i normalne. skunek: Ciało rzucono z prędkością 14,7 m/s pod kątem 30 stopni do poziomu. Obliczyć przyśpieszenie styczne i normalne ciała oraz promień krzywizny toru po 1,25 sekundy od rozpoczęcia ruchu. Oporu powietrza nie uwzględniać. (Prosiłbym prócz samych wzorów o wyjaśnienie na podstawie wektorów, wykładowca zawsze ich używa i chciałbym to w końcu zrozumieć, z góry dziękuję.)

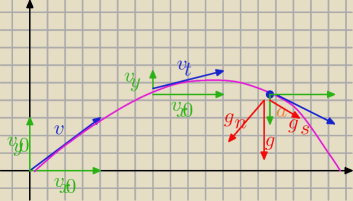
aniabb: v_x0=v*cosα = 14,7*cos30° = 14,7 * 0,866 = 12,73m/s v_y0=v*sinα = 14,7*sin30° = 14,7 * 0,5 = 7,35m/s ruch w bok jest ruchem jednostajnym v_x0 sie nie zmienia ruch w górę to ruch jednostajnie opóźniony (grawitacja g=10m/s2 (chociaż na tym poziomie to pewnie już 9,81)) v_yt=v_y0−gt = 7,35m/s − 12,5m/s= −5,15m/s tutaj minus znaczy, że wektor jest skierowany w dół prędkość ciała po czasie t v_t=√12,73²+5,15²=13,73m/s kąt α cosα=5,15/13,73 = 0,375 ⇒ α = 68° przyśpieszenie styczne g_s = g*cosα = 10*0,375=3,75m/s² przyśpieszenie normalne g_s = g*sinα = 10*0,927 = 9,27m/s² Promień krzywizny z przyśpieszenia normalnego g_n=v²/R ⇒ R=v²/g_n = 13,73²/9,27 = 20,33m