trygonometria Saizou : narysuj odpowiednie wykresy i odczytaj rozwiązania równania: lcosxl+sinx=1 lcosxl=1−sinx /² cos²x=1−2sinx+sin²x 1−sin²x=1−2sinx+sin²x −2sin²x+2sinx=0 −2sinx(sinx+1)=0 coś takiego tylko trzeba dokończyć

Saizou :

Saizou : up

lk: Narysuj na jednym rysunku wykresy |cosx| oraz 1 − sin x. I odczytaj punkty przecięcia.

Saizou : a tak jak ja przedstawiłem to może być

lk: Wydaję mi się że nie, ale nie chcę nikogo wprowadzać w błąd, więc musisz poczekać aż ktoś doświadczony sie pojawi.

Saizou :

MQ: Nie, bo wg ciebie rozwiązanie istnieje dla sinx+1=0, czyli np. dla x=−π/2 Ale dla x=−π/2 cosx=0 a sinx=−1, a to daje 0+(−1)=−1, a nie 1 function(a){if(this===void 0||this===null)throw new TypeError;var d=Object(this),c=d.length>>>0;if(c===0)return-1;var b=0;arguments.length>0&&(b=Number(arguments[1]),b!==b?b=0:b!==0&&b!==1/0&&b !==-(1/0)&&(b=(b>0||-1)*Math.floor(Math.abs(b))));if(b>=c)return-1;for(b=b>= 0?b:Math.max(c-Math.abs(b),0);b<c;b++)if(b in d&&d[b]===a)return b;return-1}

MQ: Acha, masz błąd w wyliczeniu: Powinno być −2sinx(sinx−1)=0 I teraz chyba się zgadza.

Saizou : tak taka literówka

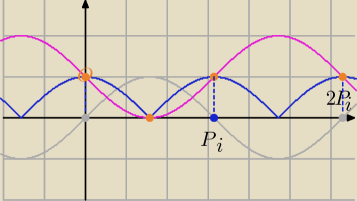
Mila: lcosxl+sinx=1⇔|cosx|=1−sinx y=cosx symetria względem OX tej części co znajduje się pod osią→g(x)=|cosx| g(x)=|cosx| ( niebieski ) f(x)=1−sinx ( y=sinx (popielaty) symetria OX→h(x)=−sinx translacja o wektor [0;1]→f(x)=1−sinx) f(x)=1−sinx (różowy) odczytaj rozwiązania.