Może mi ktoś pomoże z tymi zadaniami Kamil: 1. Cień chłopca w momencie, gdy promienie słońca padaja pod kątem 31 stopni do ziemi, ma długość 2,5 metra. Oblicz wysokość chłopca i długość cienia drzewa o wysokości 3,6m w tym samym momencie. 2. Dany jest trapez równoramienny ABCD o podstawach AB, CD. Wyznacz sinus, cosinus i tangens kąta CAB, jeśli wiadomo, że IABI=18, ICDI=12, IBCI=IADI=6

Damian: POMAGAM

Damian:

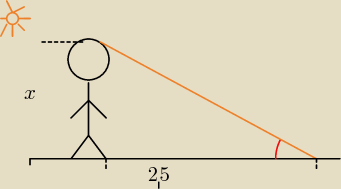
	x
tgα =		⇒ x = tgα * 2,5
	2,5

tg31⁰ = 0,60 x = 0.6 * 2,5 = 1.50 m wysokosc chlopaka to 1.5m 3,6 − wysokosc drzewa

	3,6		10
tgα = {3,6}{y} ⇒ y =		= 3,6 *		= 6m
	tgα		6

długosc cienia drzewa wynoci 6m

Damian: zad 2

Damian: Czy taki jest rysunek Czy może |AD| = |BC| = 6 czy sąto boki trapezu czy sa to jego przekątne

tim: AD oraz BC są bokami (zazwyczaj jest tak), ale mozna rozważyć dwa przypadki.

kamil: trudno mi powiedzieć. ponieważ w zadaniu nic więcej nie było podane i nie jest zaznaczone tak naprawdę czy to boki czy przekątne, ale moim zdaniem to są chyba boki

kamil: sprawdzałem w książce jak są zaznaczane wierzchołki trapezu i jest to w kolejności ABCD, czyli w Twoim rysunku nalezałoby przestawić C i D

Damian: Ok rano zamieszcze rozwiazanie

Damian: skoro BC = AD to boki wiec (rysunek) 2x = |AB| − |CD| 2x = 18 − 12 x=3 h² = c² − x² h² = 36 − 9 h = √25 h = 5

	5
sinα =
	6

	3		1
cosα =		=
	6		2

	5
tgα =
	3

kamil: Chyba jednak w tym zadaniu jest pomyłka, bo 36 − 9 = 27 , a nie 25