analityczna PuRXUTM: Prosta k przechodzi przez punkt A=(3,2) i przecina dodatnie półosie układu współrzędnych w takich punktach, że iloczyn ich odległości od punktu (0,0) wynosi 25. Znajdź równanie prostej k. Zacząłem tak k: y=ax+2−3a Obliczyłem punkty wspólne z osiami współrzędnych

	3a−2
A=(		,0) B=(0,2−3a) S=(0,0)
	a

Podstawiłem do wzoru IASI * IBSI=25 i zacząłem liczyć ale wyszła mi na końcu sprzeczność że nie ma takiego a

pigor: ... , otóż z warunków zadania wynika, że szukasz prostej ^x_a+^y_b=1 takiej że ab=25 i ³_a+²_b=1 ⇔ ab=25 i 3b+2a=ab ⇔ 3b+2a=25 i ab=25 ⇔ ⇔ 2a=25−3b i 2a*b=50 ⇒ (25−3b)b=50 ⇒ ... ⇒ b=a=5 , zatem ^x₅+^y₅=1 ⇔ x+y=5 ⇔ x+y−5=0 − szukana prosta . ...

PuRXUTM: Dzięki pigor, będę to musiał powoli rozkminiać w nagrodę że Ci się chciało

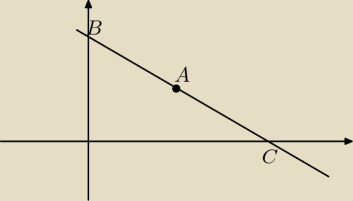
Ann: A=(3,2) B=(0,y_b) C=(x_c,0) y_b *x_c =25 k: y=ax+b 2=3a+b 0=a*x_c +b y_b=a*0+b ⇒b=y_b y_b *x_c =25 b=y_b

	2−yb
2=3a+yb ⇒a=
	3

y_b *x_c =25

	2−yb
0=xc*		+yb ⇔ 2/3xc − xc *yb /3 +yb=0 ⇔2/3 xc+yb =25/3 ⇔yb=25/3−2/3 xc
	3

x_c*(25/3−2/3x_c)=25 |*(−3/2)

	75		75
xc2−		xc+		=0
	2		2

	75		75−8		25*3*67
Δ=(75/2)2−4*(75/2)=		*		=
	2		2		4

	75   5√3*67   + 2   2
xc=
	2

reszte niewiadmych wyliczasz podstawiajac do odpowiednich rownan

PuRXUTM: dzięki Ann