Wykaż, że pyto7: Jeżeli w trójkącie o bokach a, b, c środkowe porpowadzone na boki a i b przecinają się pod kątem prostym, to c²=¹₅(a²+b²)

pyto7: →Δ←

colo: Zastosuj dwa razy twierdzenie Pitagorasa do odpowiednich trójkątów, pamiętając o tym, że środkowe przecinają się w stosunku 2:1.

pyto7: Mam zastosować twierdzenie Pitagorasa posiadając tylko 1 bok?

pyto7: Aaaa.. Ogarniam

pyto7: Dzięki

colo: Proszę

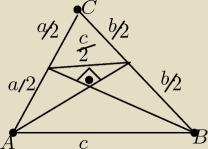
Vax: Nie trzeba korzystać z tego, że środkowe przecinają się w stosunku 2:1, wystarczy sam Pitagoras i fakt, że odcinek łączący środki dwóch boków w trójkącie jest równy połowie długości 3 boku

	c		a		b		1
c2 + (		)2 = (		)2+(		)2 ⇔ c2 =		(a2+b2) cnd.
	2		2		2		5