baaaaaardzo prosze o pomoc miska: baaaardzo prosze o pomoc punkty A=(−2,12) i B(6,−2) sa wierzchołkami trójkąta prostokątnego abc o kacie prosttym przy wierzchołku C. oglicz wspolrzedne C wiedzac ze lezy on na prostej o rownaniu x+3y=22. rozważ wszystkie przypadki

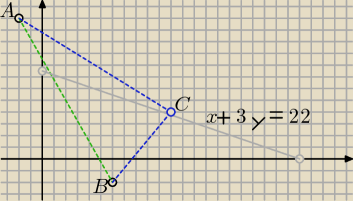
dero2005: oblicz długość odcinka AB, BC, AC podstaw do pitagorasa i ułóż układ równań z drugim równaniem x + 3y = 22

dero2005: mnie wyszło C₁(10, 4) C₂(−5, 9)

miska: jak oblicze BC i AC skoro nie mam wspołrzednych C

aniabb: wstawisz C(22−3y ; y) i będziesz miała równanie z niewiadomą y

miska: i tak jak pisał dero2005 obliczyc odcinek BC i AC z takimi wspołrzednymi C?

PuRXUTM: tak

miska: i wyjdzie mi, ze AB to √260 a BC √256−96y+9y²+√y² +4y+4 ? ... i?

aniabb: pitagorasa

miska: z taka postacia odcinka BC?

miska: z taka postacia odcinka BC?

aniabb: BC to 1 pierwiastek z tej sumy

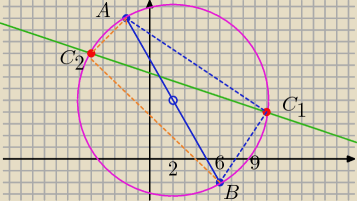
Mila: A=(−2,12) i B(6,−2)

	1		22
k: y=−		x+
	3		3

AB jest przeciwprostokątną. Obliczam wsp. Srodka AB

	−2+6		12+(−2)
S=(xs;ys)=(		;		)=(2;5)
	2		2

równanie okręgu o środku (2,5) i r=√65 (x−2)²+(y−5)²=65 Punkt C to punkt przecięcia okręgu i prostej; x+3y=22⇔x=22−3y (22−3y−2)²+(y−5)²=65 po rozwiązaniu: y₁=4 lub y₂=9 x₁=22−3*4=10 lub x₂=22−3*9=22−27=−5 stąd C₁=(10;4) i C₂=(−5;9) Kąty C są proste jako wpisane w okrąg oparte na średnicy

miska: dziękuje

Mila: Proszę, wszystko jasne?