coś dla ambitnych (proszę o pomoc) jadzia: Objętość ostrosłupa prawidłowego trójkątnego jest równa 6√3, a kąt nachylenia krawędzi bocznej do podstawy wynosi 30° . Oblicz długość krawędzi bocznych.

jadzia: ktoś ma jakiś pomysł sorry za spam..

dero2005: V = 6√3

	2
a =		√3hp
	3

	a2√3		hp2√3
V =		=
	4		3

	Pp*h
V =		= 6√3
	3

P_p*h = 18√3 h_p²*h = 54

h		√3
	= tg 30o =
2   hp 3		3

	2
h =		√3hp
	9

	2
hp2*		√3hp = 54
	9

h_p³ = 81√3 h_p = ³√81√3

2   hp 3		√3
	= cos 30o =
l		2

	4√3		4√3
l =		hp =		*3√81√3 = 4
	9		9

dero2005: w trzecim wzorze zamiast tego co jest powinno być

	a2√3
Pp =
	4

Stig: Sorry, że bez rysunku, ale nie działa mi ta opcja. (nie wiem czemu) Narysowałem tę figurę, a następnie oznaczyłem jej krawędź podstawy jako 'a', a wysokość graniastosłupa jako 'h'. Rysując obok trójkąt prostokątny o wysokości 'h' i kątem 30 stopni miedzy krótką przyprostokątną, a przeciwprostokątną widzę, że jest to trójkąt "szczególny" (katy 30,60,90). Teraz już wiem, że poszukiwana długość krawędzi bocznej ma dł. '2h', a krótka przyprostokątna 'h√3'. Objętość V=1/3 Pp*h − Pp − pole podstawy Pp=1/2*a*h√3 Podstawiam V=1/3*1/2*a*h√3*h Teraz do szczęścia brakuje mi dł. 'a', więc próbuje uzależnić jakoś 'a' od 'h'. Patrzę na kawałek podstawy całej figury i mam trójkąt równoramienny o podstawie 'a' i ramionach h√3. Kąty w tym trójkącie to 120 i 30 stopni. Dziele ten trójkąt na dwie równe części i znowu mam trójkąt szczególny o dł. 1/2a i hp[3]. teraz mogę odczytać, że 1/2a=3/2h, więc a=3h. Teraz mam już wszystko i podstawiam V=1/3*1/2*a*h√3*h V=1/3*1/2*3h*h√3*h h³=V*2/3 * 1/√3 V=6√3 − z treści zad. h³=4, więc h=³√4 szukana krawędź ma dł. '2h', wiec ostatecznie 2*³√4

patryk:

	2
dero co to za wzor		√3hp?
	3

patryk: i skad sie wzial?

patryk: prosze powiedzcie tylko skad sie to wzielo i bedzie wszystko jasne

dero2005:

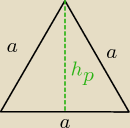
	4a2−a2		3a2
hp = √a2 − (a2)2 = √a2 − a24 = √		= √		=
	4		4

	a
		√3
	2

to było z pitagorasa , teraz liczymy a w zależności od h_p

	a
hp =		√3 |*2
	2

2h_p = a√3 |: √3

	2hp		√3		2
a =		*		=		√3hp
	√3		√3		3