zaznacz na osi liczbowej zbiór rozwiazań nierówności: 3*Ix+3I≥3+Ix+3I evitte: zaznacz na osi liczbowej zbiór rozwiazań nierówności: 3*Ix+3I≥3+Ix+3I

ZKS:

	3
|x + 3| ≥
	2

Mati_gg9225535: najpierw ją trzeba rozwiazac wiec 2 przypadki 1^o x+3≥0 ⋀ 3*(x+3) ≥ 3+(x+3) 2^o x+3<0 ⋀ 3*(−x−3) ≥ 3+(−x−3) na koncu czesc wspólną

Mati_gg9225535: albo tak jak ZKS proponuje

ZKS: Przypadki zbędne.

ZKS: Zresztą jak to zawsze mówię jak kto woli.

evitte: nie ogarniam bo ja bym to jakoś obliczyła...wszystko na 1 strone itd...

evitte: a czemu 3/2 ?

Mati_gg9225535: tak to od razu rozpisuje i licze a zanim sie zastanowie to tyle minieczasu ile bym poswiecil na ich rozwiazanie tym bardziej ze tu tylko dwa no ale racja nie zwrocilem uwagi na to by przenieść to |x+3| na lewo a to sprawę ułatwiło

ZKS: Skoro nie widać podstawić sobie |x + 3| = t ≥ 0 3t ≥ 3 + t 3t − t ≥ 3 2t ≥ 3

	3
t ≥
	2

	3
|x + 3| ≥
	2

Mati_gg9225535: 3*Ix+3I≥3+Ix+3I 3*|x+3|−|x+3|≥3 (3 − 1 = 2 ) 2*|x+3|≥3 // 2

	3
|x+3| ≥
	2

agi: ¦x+3¦<2

bezendu: x+3<2 i x+3>−2 x<−1 i x>−5 x∊(−5,−1)

agi: Zaznacz na osi liczbowej i zapisz w postaci przedzialow rozwiązania nierówności A=¦3−x¦<2 B=¦x+2¦≥4

agi: Rozwiąż równanie A=(x+3)⁻4=(x−2)(x+2)−7x

bezendu: @agi załóż nowy temat

agi: Zaznacz na osi liczbowej i zapisz w postaci przedziałów rozwiązania nierówności a). [3−x]<2 b). [x+2]≥4

agi: Zaznacz na osi liczbowej i zapisz w postaci przedziałów rozwiązania nierówności a). [3−x]<2 b). [x+2]≥4

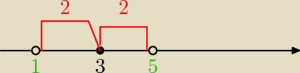
krystek: a)Ix−3I<2⇔x∊(1,5)

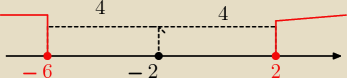
krystek: Ix+2I≥4⇔x∊(−∞,−6> U<2,∞)