 xa = 8
ya = −3
xc = 10
yc = 11
|AC|=√ ( xc − xa )2 + ( yc − ya )2
|AC|=...
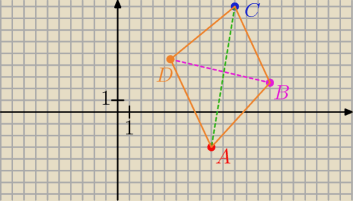
na początek policz długość przekątnej.
Uwaga...ten rysunek jest tylko poglądowy, więc za bardzo się nim nie sugeruj.
xa = 8
ya = −3
xc = 10
yc = 11
|AC|=√ ( xc − xa )2 + ( yc − ya )2
|AC|=...
na początek policz długość przekątnej.
Uwaga...ten rysunek jest tylko poglądowy, więc za bardzo się nim nie sugeruj.
| 1 | ||
P = | * |AC| * |BD| | |
| 2 |
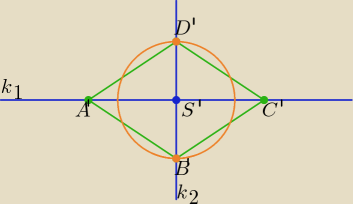 Przedstawiam pewien sposób rozwiązywania zadań z geometrii analitycznej polegający
na takim umiejscowieniu rozpatrywanego obiektu (tu rombu) w układzie współrzędnych,
aby rachunki stały się prostsze.
|AC| = √22 + 142 = √200 = 10√2
Przedstawiam pewien sposób rozwiązywania zadań z geometrii analitycznej polegający
na takim umiejscowieniu rozpatrywanego obiektu (tu rombu) w układzie współrzędnych,
aby rachunki stały się prostsze.
|AC| = √22 + 142 = √200 = 10√2
| 1 | 1 | √2 | ||||
Pole rombu | *|AC|*|BD| = 10 ⇒ | *10√2*|BD| = 10 /* | ⇒ |BD| = √2 | |||
| 2 | 2 | 10 |
| 8+10 | −3+11 | |||
S = ( | , | ) = (9, 4) | ||
| 2 | 2 |
| 14 | ||
k1 − prosta zawierająca punkty A'(−1, −7) i C'(1, 7): y = a1x, a1 = | = 7 | |
| 2 |
| 1 | ||
k2 − prosta zawierająca punkty B', S' i D': y = a2x , k2⊥k1 ⇒ a2 = − | , | |
| 7 |
| 1 | ||
k2: y = − | x | |
| 7 |
| 1 | √2 | 1 | ||||
Tworzymy okrąg o środku S'(0, 0) i promieniu |B'S'|=|S'D'|= | |BD|= | = | ||||
| 2 | 2 | √2 |
| 1 | ||
x2 + y2 = | ||
| 2 |
| 1 | 1 | 49 | ||||
Rozwiązujemy równanie: x2 + (− | x)2 = | ⇒ x2 = | ||||
| 7 | 2 | 100 |
| 7 | 1 | 7 | 1 | 7 | 1 | |||||||
x = − | i y = − | *(− | ) = | ⇒ B' = ( − | ; | ) | ||||||
| 10 | 7 | 10 | 10 | 10 | 10 |
| 7 | 1 | 7 | 1 | 7 | 1 | |||||||
x = | i y = − | * | = − | ⇒ D' = ( | ; − | ) | ||||||
| 10 | 7 | 10 | 10 | 10 | 10 |

