W trójkącie równoramiennym ABC podstawa AB ma długość 26 cm... Nieznajoma: W trójkącie równoramiennym ABC podstawa AB ma długość 26 cm. Długość wysokości AE jest równa 24 cm. Oblicz: a) obwód trójkąta ABC b) długośćodcinków, na jakie wysokość CD podzieliła wysokość AE c) stosunek pola trójkąta ADS do pola trójkąta CSE, gdzie S jest punktem wspólnym wysokości AE i CD.

Nieznajoma: Proszę o pomoc...

Basia: Pomagam. Rysuję

Basia: Pomagam. Rysuję

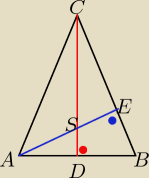
Basia: AB=26 AD = BD = ¹₂AB = 13 AE = 24 AB² = AE² + BE² 26² = 24² + BE² BE² = 26² − 24² = 676−576 = 100 BE = 10 △BEA ~ △BDC (uzasadnij !) ^BE_BD = ^AB_BC ¹⁰₁₃ = ²⁶_BC 10*BC = 13*26 BC = ^13*26₁₀ = ^13*13*2₁₀ = ¹⁶⁹₅ L = AB + 2*BC = 26 + ^2*169₅ policz do końca ! ^BE_BD = ^AE_CD ¹⁰₁₃ = ²⁴_CD 10*CD = 24*13 CD = ^2*12*13₁₀=^12*13₅ policz do końca! △ADS ~ △AEB ^AS_AD = ^AB_AE ^AS₁₃=²⁶₂₄=¹³₁₂ AS = ^13*13₁₂=¹⁶⁹₁₂ ES = 24−¹⁶⁹₁₂ = ^24*12−169₁₂ policz do końca ! △ADS ~ △CES s = ^AD_CE CE = BC−BE = ¹⁶⁹₅−10 = ¹⁶⁹⁻⁵⁰₅ = ¹¹⁹₅

PADS
	= (1195)2
PCES

sprawdź czy się nie pomyliłam w rachunkach

Nieznajoma: Dziękuję

dfsdfd: βββ

ryuruy: ββββδγα∊→⇒≈⇔→⇔≈