Funkcje asd: Podaj zbiór wartości:

	1
f(x) =		. Dziedzinę obliczyłem, co dalej? jakieś wskazówki?
	|x|+2

asd: pewno trzeba będzie rozpatrzyć to w dwóch przedziałach, tak?

asd: x ≥0 i x < 0 \{2}

ewa: |x|≥0 /+2 |x|+2≥2

	1		1
zatem		≤		oraz dodatnie!
	|x|+2		2

zbiór wartości=(0,¹₂>

aniabb: a wiesz kiedy ta funkcja będzie największa?

ewa:

	1
Jak chcesz z wykresu to narysuj wykres funkcji dla x≥0 : f(x)=		, a następnie
	x+2

odbij go symetrycznie względem osi y (zauważ, że funkcja podana przez ciebie jest parzysta!) Co do dziedziny to D=R

asd: Ogolnie to słabo to rozumiem... Po pierwsze dlaczego D = R ?

asd: szczerze mowiac to nawet nie wiem jak sie zabrac za to zadanie

asd: Więc?

aniabb: a znasz jakiś x żeby mianownik był =0

ewa:

	1
Bo za x możesz wstawić dowolną liczbę rzeczywistą i wyrażenie		będzie miało sens
	|x|+1

ewa:

	1
Przepraszam wyrażenie
	|x|+2

asd: Okej, a co dalej zrobić z tym przykladem? Jak sie zabrac do tego typu zadan?

asd: Wiem, ze go rozwiazaliscie, ale jak?

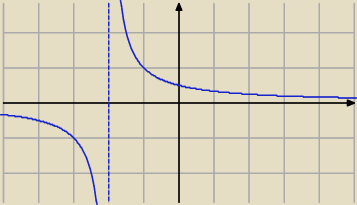
Bogdan: Można spróbować sporządzić wykres w następujący sposób:

	1
Najpierw szkicujemy y =
	x + 2

Potem wymazujemy wykres po lewej stronie osi y i wrysowujemy w to miejsce odbicie od osi y wykresu leżącego po prawej stronie osi y.

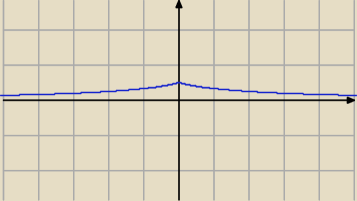
Bogdan: Końcowy wykres jest taki. Teraz można odczytać zbiór wartości funkcji f(x). Przedstawiony sposób jest jedynie ilustracją zadania. Zadanie wymaga jednak analitycznego rozwiązania.

aniabb: taka funkcja będzie największa, gdy mianownik będzie najmniejszy

aniabb: a potem zastanowić się co się dzieje jak mianownik rośnie

ewa:

	1
Jeżeli chodzi o narysowanie funkcji f(x)=		dla x≥0 (wówczas |x|=x) to zrób sobie
	x+2

tabelkę i podstawiaj za x kolejno 0,1,2,3,4,... do wzoru i wyliczaj y i zaznacz w układzie współrzędnych

	1
0 →
	2

	1
1→
	3

	1
2→
	4

..... itd

	1
biorąc coraz większe x ułamki stają się coraz mniejsze (limx→∞		=0 ) wykres zbliża się
	x+2

coraz bardziej do osi x. Drugą część wykresu (dla x<0) dostaniesz odbijając powyższy wykres symetrycznie względem osi y. Z wykresu możesz odczytać wartości (wartości funkcji odczytujemy na osi Y!)

asd:

	1
A taki przykład: f(x) =		to będzie:
	x2+1

1
	≤ 1 czyli y∊(0 ; 1>
x2+1

aniabb: tak

asd: a dlaczego jak na poczatku bylo x²≥0 to później znak nierownosci zmienia się?

asd: A taki przykład?

	⎧	1 dla |x|<1
f(x) =	⎨
	⎩	4 dla |x| ≥ 4

asd: hm?

asd: A tu nie bedzie przypadkiem 1 i 4

aniabb: brawo

asd: dzieki xd, a gdyby zamiast 1 dla |x|<1 byłoby x dla |x|<1, to ZW = <0;1) u {4} ?

qwerty: hmm?

asd: hmm?

aniabb: tak

asd: Okej, dzięki

asd: A w przykladzie f(x) = √2(1−cosx) odpowiedzią bedzie y∊ <−1;3>

asd: tzn gdyby nie ten pierwiastek