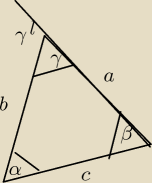
Wykazać, że w trójkącie o kątach α, β, γ zachodzi warunek sin γ = sin (α+β). gigio: Wykazać, że w trójkącie o kątach α, β, γ zachodzi warunek sin γ = sin (α+β). z tego co pamiętam, to z sumy kątów w trójkącie γ=180˚−(α+β) z sumy 2 kątów przyległych γ'= 180˚−γ oraz γ'=α+β

gigio: udało mi się to rozwiązać samemu. wrzucam bo może komuś się przyda z twierdzenia o sumie kątów w trójkącie α+β+γ=180˚ a zatem γ=180˚−α−β co można też zapisać jako γ=180˚−(α+β) zakłamy, że λ=α+β i podstawiamy do wcześniejszego wzoru co daje γ=180˚−λ wobec tego sin γ = sin (180˚−λ) a ze wzorów reducyjnych sin (180˚−λ) = + sin λ wobec tego sin γ = + sin λ a z wcześniejszego założenia λ=α+β i tym samym sin γ = sin (α+β) co należało udowodnić