zadanie daniel: narysuj zbior punktow na plaszczyznie ; |z+1|+|z−1|=2 jak to rozwiazac ?

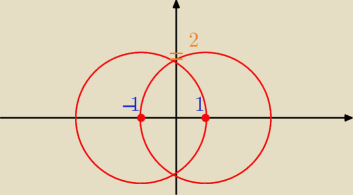
daniel: czy to bedzie cos takiego ?

Godzio: Chyba nie, przeczytaj sobie co to jest elipsa

daniel: wiem co to elipsa pomoz rozwiazac , jak rozwiazesz szybciej to zrozumiem

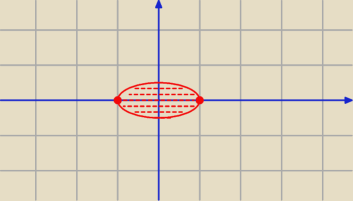
Godzio: No to jakie masz tu punkty ? (−1,0) i (0,1). Elipsa to zbiór punktów, których suma odległości od dwóch ustalonych punktów jest stała. No to masz już odpowiedź. Oczywiście to jest krawędź + to co w środku

daniel: |z−z₁|+|z−z₂|=l powstanie elipsa (z₁ , z₂, l ) i teraz jak rysujemy taką elipse ?

daniel: no i jasne , dzieki

daniel: tylko jeszcze jedno , skad wiemy jak szeroka ona bedzie ?

Godzio: Chwila, chwila, bo teraz ja coś popsułem.

daniel: bo tak jak napisalem powstanie elipsa z₁ z₂ i l do czego nam sie przydaje te " l "

daniel: wedlug mnie to zazanaczam te pkt x=1 i x=−1 szukam najblizeszgo miejsca w ktorym sie spotkaja i to wyznaczy mi wysokosc tej elipsy ,tak samo w drugą strone

daniel: tzn miejsca w ktorym proste przechodzace przez te pkt sie spotkaja zle to wyrazilem

daniel: zreszto juz sam nie wiem ...

daniel: albo rysuje kola w tych pkt i przeciecia tych kol mi wyznaczaja to

Godzio: A dobra, jest ok, miałem moment zwątpienia

	1
Koła akurat tego nie wyznaczają, ja akurat zauważyłem, że (0,		) będzie najwyżej położonym
	2

punktem. Hmm a jak to wyznaczyć ? Trzeba byłoby się pobawić wzorkami.

daniel: zdradzisz tajemnice jakimi ?

daniel: a przypadkiem to nie bedzie punkt (0, √3 ) ?

Godzio:

(x − x0)2		(y − y0)2
	+		= 1
a2		b2

Mamy, że x₀ = y₀ = 0, oraz 2a = 2 ⇒ a = 1 (2a − "długość elipsy", inaczej oś wielka)

	y2
x2 +		= 1. I teraz trzeba znaleźć jakikolwiek punkt należący do naszej elipsy.
	b2

	1
Tutaj możemy wziąć (0,		) bo po wstawieniu do początkowego równania, wiemy, że spełnia.
	2

	1		1		1
0 +		= 1 ⇒ b2 =		⇒ b = ±		i mamy skrajne punkty.
	4b2		4		2

jak chcesz mogę Ci napisać parę faktów dotyczą elipsy, o ile Ci się to przyda

Godzio: Nie, bo odległość punktów (1,0) i (−1,0) do (0,√3) to 2, a wtedy 2 + 2 ≠ 2

daniel: przyda sie wielkie dzieki

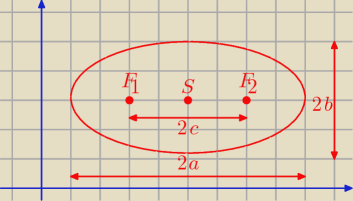
Godzio: F₁,F₂ − ogniska S(x₀,y₀) − środek elipsy 2a − oś wielka 2b − oś mała 2c = |F₁F₂| − ogniskowa Równanie elipsy przy tych danych ma postać:

(x − x0)2		(y − y0)2
	+		= 1
a2		b2

Oraz współrzędne ognisk: F₁ = (x₀ − c, y₀), F₂ = (x₀ + c, y₀) I zachodzi zależność: c² = a² − b²

	c
Jeszcze jest coś takiego jak mimośród elipsy: ε =
	a

daniel: skąd ta nierownosc 2+2 ≠ 4

	√5
u Ciebie odleglosc do punktu (0 , 12) wynosci
	2

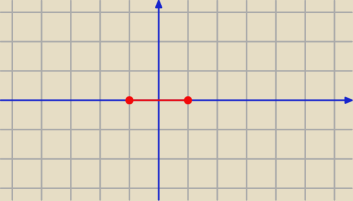
Godzio: Wiesz co ... ja już chyba nie myślę, Przecież to o co nas pytają to ten odcinek ...

Godzio: Sory, za to wszystko, owszem jest to dosyć abstrakcyjna elipsa, bo ogniska są na skraju, gdyby było chociażby: |z − 1| + |z + 1| = x, a x byłby dowolną liczbą > 2 to już była by elipsa ... A tutaj mamy elipsę zdegenerowaną do odcinka, obawiam się, że chyba pora odpocząć...

daniel: niee . dobrze przeciez zrobiles , to jest elipsa

daniel: w takim razie skąd Ci ten punkt wyszedl (0, ¹₂ ) ?

Godzio: Bo rozważając równanie elipsy zakładamy, że a i b są różne od zera. Dlatego coś wyszło