dziedzina adaś: Dana jest funkcja f(x ) = |x− 1|− |x + 2| dla x ∈ R . Podziel dziedzinę na trzy przedziały Jak mam to zrobić , pomożecie ?

Artur_z_miasta_Neptuna: 1 przedział: kiedy (x−1) <0 oraz (x+2) <0 2 przedział: kiedy (x−1) <0 oraz (x+2) ≥0 3 przedział: kiedy (x−1) ≥0 oraz (x+2) ≥0

adaś: wyszło mi 1.(−2,1) 2.<−2,1) 3.<−2,1> dobrze?

Artur ..... : źle ! podstawa: suma tych przedziałów ma dać Ci R ... czyli przedział (−∞, +∞) te przedziały NIE MOGĄ mieć ze sobą części wspólnych

Artur ..... : z tego co napisaleś ... wyszło, że: dla x=0 (x−1) jest zarówno mniejszy jak i większy od 0 (x+2) jest zarówno mniejszy jak i większy od 0 gdzie tu logika

adaś: ja w ogóle nie wiem jak to rozpatrywać , pomożesz mi to poprawnie zapisać ?

adaś: może ktoś to po kolei rozpisać jak robi ?

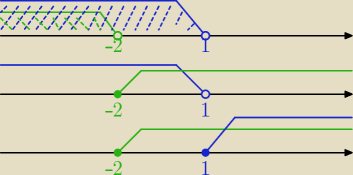
Artur ..... : masz rozpisane te 3 warunki (kazda na innej osi) ... już wiesz jak to zrobić

adaś: dziękuje Tobie za te rysunki, teraz to będzie od (−∞,2) U <2,1) U <−2,∞)

Artur ..... : yyyyy w sensie 1 warunek jest gdy x∊(−∞,2) 2 warunek gdy x∊<2,1) 3 warunek gdy x∊<−2,∞) więc dla x∊(−∞,2) masz f(x) = −(x−1) − −(x+2) x∊<2,1) masz f(x) = −(x−1) − (x+2) x∊<−2,∞) masz f(x) = (x−1) − (x+2)