sefsefs
karolajn: Wielomian w(x) jest trzeciego stopnia i ma trzy pierwiastki: sin 5/6π , sin7/6π, sin 11/6π.
Wiadomo, że w(1)= −3/8. Rozwiaż nierówność W(x) (x−2)>0
2 lis 22:42
wmboczek: zaznaczasz 4 liczby (pierwiastki) i rysujesz W(1) pozwala ustalić że od dołu
2 lis 23:40
Mila: | | 1 | | 1 | | 3 | | 9 | | 3 | | 1 | |
W(1)=a(1− |
| )*(1+ |
| )2=− |
| ⇔a* |
| =− |
| ⇔a=− |
| |
| | 2 | | 2 | | 8 | | 8 | | 8 | | 3 | |
| | 1 | | 1 | | 1 | |
w(x)=− |
| *(x− |
| )*(x+ |
| )2 |
| | 3 | | 2 | | 2 | |
| | 1 | | 1 | | 1 | |
W(x) (x−2)>0⇔− |
| *(x− |
| )*(x+ |
| )2*(x−2)>0⇔ |
| | 3 | | 2 | | 2 | |
dokończ
2 lis 23:49
karolajn: ot nie musze uwzgledniac 1/3 ?
3 lis 09:48
karolajn: Ponawiam pytanie. Wszystko rozumiem tylko nie pamietam jakie byly zasady rysowania w takich
nierownosciach. Pomija się poprostu "a" ? Bo a=1/3, chyba ?
4 lis 14:59
Mila:
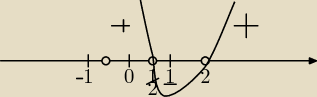
a<0 i dlatego pomnożyłam obie strony przez (−1)
jeśli a>0 to nie ma wpływu na znak iloczynu i pomijamy 1/3 a także (x+1/2)
2 bo jest nieujemne.
| | 1 | | 1 | | 1 | |
(x− |
| )*(x−2)<0 i x≠− |
| ⇔x∊( |
| ;2) |
| | 2 | | 2 | | 2 | |
4 lis 15:11
karolajn: Rozumiem. Poprostu nie wiedziaal co robic z jakas liczba przed nawiasami z miejscami zerowymi.
Pomijamy je (oczyw. wieksze od 0
4 lis 15:31
Mila: 
4 lis 15:36
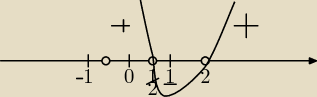 a<0 i dlatego pomnożyłam obie strony przez (−1)
jeśli a>0 to nie ma wpływu na znak iloczynu i pomijamy 1/3 a także (x+1/2)2 bo jest nieujemne.
a<0 i dlatego pomnożyłam obie strony przez (−1)
jeśli a>0 to nie ma wpływu na znak iloczynu i pomijamy 1/3 a także (x+1/2)2 bo jest nieujemne.
