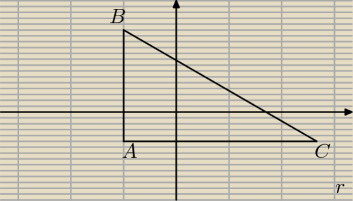
równania prostych kiki: przyprostokątne trójkata prostokątnego abc zawierają się w prostych równoległych do osi ukladu współrzędnych. wyznacz równania prostych zawierających boki tego trójkata jesli B(−2,5) C(10,−1). Rozwiązanie(opisuje przypadek pierwszy): równanie prostej CB: y=−1/2x+4 bo przechodzi przez punkt C i B a mamy ich wspólrzedne. równanie pr: AC, y=−1 , bo mamy punkt C oraz wiemy, że ta prosta jest równoległa do OX równanie prostej AB, równoległej do OY i przechodzącej przez punkt B. wychodzi mi y=2a=b ? i co jest źle? musi być x=−2

aniabb: AB x=a podstawiam punkt B(−2,5) −2=a więc x=−2

aniabb: nie można napisać wzoru w postaci y=ax+b do prostej rownoległej do osi OY bo to nie jest funkcja

...: To napisz f(x)=ax+b