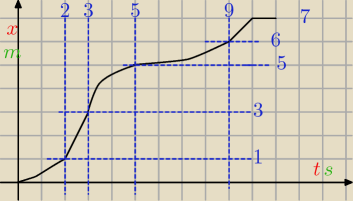
.. asdf: fizyka Na zielono − jednostki Punkt materialny porusza się po prostej w kierunku rosnących x. Na rysunku przedstawiono jego zależność położenia od czasu. Obliczyć: 1. średnią prędkość dla całego ruchu 2. prędkość maksymalną 3. średnie przyspieszenie dla pierwszych 5 sekund. x₀ = 0

	Δx		7
1. Średnia prędkośc to po prostu V =		=		m/s
	Δt		9

2. Prędkośc maksymalna −−−−jak z wykresu to policzyć? 3. średnie przyspieszenie dla pierwszych 5 sekund:

	x5 − x0
Vśr0→5s =		= 1m
	5s

	1
asr =		?
	5

aniabb: v_śr=7/11

asdf: tak a jak będzie z prędkością maksymalną?

aniabb: v_max=2m/s

aniabb: między 2 a 3 sek

aniabb: najbardziej stromy kawałek krzywej

asdf: V_max dla t_2→3s będzie?

asdf: ok, dzięki, teraz postaram się z tego narysować przyspieszenie

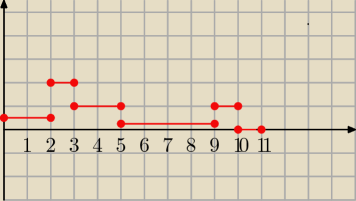
asdf: dobrze?

aniabb: jeśli myślałeś o prędkości to w miarę ... musisz podzielić na mniejsze kawałki na tych łukach

asdf: chodziło mi o przyspieszenie

asdf: to źle?

aniabb: jesteś w połowie..drugi raz to samo i będzie przyśpieszenie

asdf: Czyli nie rozumiem...

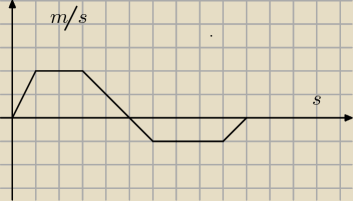
asdf: zacznę od łatwiejszego

aniabb: ten jest milutki... z tego przyśpieszenie ci wyjdzie jak przed chwilą próbowałeś

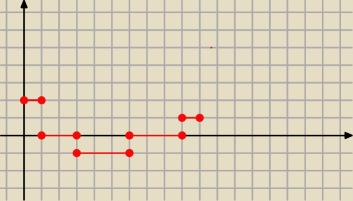
asdf: to jest przyspieszenie tak?

aniabb: brawo

asdf: Teraz spróbuję to opisać, czy dobrze myślę: W pierwszej sekundzie jest już na drugiej sekundzie, ma przyspieszenie: 2m/s (od postoju do ruchu) Dla t ∊ <1,3> porusza się ruchem jednostajnym, jego prędkość to 2m/s, a przyspieszenie jest równe 0. Prędkość w 4 sekundzie to 1 m/s, czyli zwalnia...jego przyspieszenie to −1 m/s. W piątej sekundzie przez "ułamek" sekundy zatrzymuje się, jego v = 0, a = −1. Od piątej sekundy zaczyna się cofać. jego prędkość to −1m/s ale do tyłu, a = −1. Od 6 sekundy do 9 sekundz cofa sie ze stałą prędkością V = −1 m/s, a = const. W ostatniej sekundzie hamuję, czyli zmienia prędkość z −1m/s na postój (0m/s), a jego przyspieszenie w tym momencie wynosi a = 1m/s Dobrze rozumiem?

aniabb: tak ..tylko wszędzie zamiast słowa prędkość używaj zmiana prędkości

aniabb: i jak stała prędkość to a=0 przy słowie const zazwyczaj myślimy o różnej od zera

aniabb: W pierwszej sekundzie ma przyspieszenie: 2m/s (od postoju do ruchu) Dla t ∊ <1,3> porusza się ruchem jednostajnym, jego prędkość to 2m/s, a przyspieszenie jest równe 0. zmiana Prędkość w 4 sekundzie to 1 m/s, czyli zwalnia...jego przyspieszenie to −1 m/s. W piątej sekundzie przez "ułamek" sekundy zatrzymuje się, jego v = 0, a = −1. Od piątej sekundy zaczyna się cofać. jego zmiana prędkość to −1m/s ale do tyłu, a = −1. Od 6 sekundy do 9 sekundz cofa sie ze stałą prędkością V = −1 m/s, a =0. W ostatniej sekundzie przyśpiesza, czyli zmienia prędkość z −1m/s na postój (0m/s), a jego przyspieszenie w tym momencie wynosi a = 1m/s

asdf: Teraz jego przemieszczenie: Od S₀ do S₅ porusza się do przodu, czyli wykres będzie rósł:

	at2		2*1
S0 →1s =		=		= 1
	2		2

S_{1 →3s} = tutaj policzę polem = 4. Czyli jest to wektor: (3,4) < ruch jednostajny (a = 0) czyli kąt 45^o S_3→5 = pole wychodzi: 2 * 2 / 2 = 2, wektor: (2,2) Od t = 5s "samochód" zaczyna się cofać, czyli wykres będzie w dół: S_5→6 = pole wychodzi: 1 *1/2 = 1/2, wektor (1,−1/2), a = −1 S_6→9 = pole wychodzi: 3, wektor = (3,3) a = 0, kąt 45^o S_9→10 = pole wychodzi: 1/2, zwalnia do postoju. Jego cała droga to 7+ 4 = 11 m jego przemieszczenie to 3m tak?

asdf: ?

aniabb: tak..ale łatwiej liczyć kratki pod wykresem prędkości niż zrozumieć co piszesz

asdf: staram się to zrozumieć dobrze Punkt materialny porusza się zgodnie z równaniem: x(t) = At − Bt², gdzie: A = 3 cm/s

	1
B =		cm/s2
	2

znajdź V(t) i a(t) b) śr. prędkośc w ciągu 0−6 s c) śr. prędkość w ciągu 3−8 s −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− x(t) = At − Bt²

	at2
x(t) = x0 + V0 +
	2

x₀ − przemieszczenie początkowe, czyli = 0 V₀ = A − prędkość początkowa, czyli = 3cm/s I teraz mam taki zapis, którego nie rozumiem:

a
	= −b → a = −2b <<< z kąd to się wzięło?
2

(t¹)' = 1 (t²)' = 2t

aniabb: to co stoi przed t² a/2 we wzorze ogólnym'' −B w zadaniu więc a/2 = −B

asdf:

	dx
Vt =		= A * 1*t0 − B * 2t1
	dt

a co z tym dt?

aniabb: nic ..mówi nam po jakiej zmiennej liczymy pochodną

asdf:

	dV
a(t) =		= (A − 2Bt)' = 0 − 2B * 1 *t0
	dt

To dół zawsze się omija?

aniabb: tak

aniabb: df/dx = f' po prostu inny zapis .. przydatny potem jak funkcje wielu zmiennych

asdf: prędkośc − droga po czasie szybkość − przemieszczenie po czasie

aniabb: odwrotnie

asdf: szybkość = V prędkość = |V|

	at2		1m
x(6) = x0 + V0t +		= At − Bt2 = 3cm/s*6s −		* 36s2 = 18 − 18 = 0
	2		2s2

	x(6) − x0		0 − 0
Vśr0−6s =		=		= 0
	6		6

średnia prędkosć_3−6s =

	9
x(3) = 3*3 −		= 4,5
	2

	64
x(8) = 8*3 −		= 24 − 36 = −12
	2

	9
I tutaj jeden punkt na osi to (3,		) a drugi to: (8,−12)
	2

Jak obliczyć pole nad osią OX i pole pod osią OX skoro nie znam miejsca zerowego?

asdf: szybkość = V prędkość = |V|

	at2		1m
x(6) = x0 + V0t +		= At − Bt2 = 3cm/s*6s −		* 36s2 = 18 − 18 = 0
	2		2s2

	x(6) − x0		0 − 0
Vśr0−6s =		=		= 0
	6		6

średnia prędkosć_3−6s =

	9
x(3) = 3*3 −		= 4,5
	2

	64
x(8) = 8*3 −		= 24 − 36 = −12
	2

	9
I tutaj jeden punkt na osi to (3,		) a drugi to: (8,−12)
	2

Jak obliczyć pole nad osią OX i pole pod osią OX skoro nie znam miejsca zerowego?

asdf: ?

aniabb: masz drogę, więc nie liczysz pola ... x(8)−x(3) /5 =−16,5/5 = −3,3m/s

aniabb: 64/2=32 x(8)=24−32=−8

asdf: http://postimage.org/image/8549b4wwb/ tak też się dało zrobić, żeby dodać te dwa pola? Oczywiscie zamiast −12 jest −8

aniabb: też można ale wtedy to ma być wykres prędkości od czasu więc liczysz v(3) i v(8) i pole pod prostą

aniabb: tzn tu nad prostą http://www.wolframalpha.com/input/?i=integral++3-x+from+3+to+8

aniabb: a jak masz drogę to po prostu −12,5/5 = −2,5

asdf: Żeby obliczyć przemieszczenie po czasie, czyli prędkość to rysuję coś podobnego jak w poście z 22²⁵ i liczę z tego pole między osią OX?

aniabb: nie..to już wykres drogi tu po prostu dzielisz przyrost drogi przez przyrost czasu .. kratki liczy się z wykresu prędkości (21:58) i wtedy mamy drogę

aniabb: v=a*t v= pole pod krzywą przyśpieszenia s=v*t s= pole pod krzywą prędkości −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− v=Δs/Δt v= pochodna drogi ..przyrost/przyrost a=Δv/Δt a= pochodna prędkości ..przyrost/przyrost

asdf: Dzięki, nie wiem czemu, ale coś nie może mi to wejść w głowę....Chyba za dużo dzisiaj i wszystko na raz (macierze, sprawozdanie, teraz to...)

aniabb: str 4 http://images.nexto.pl/upload/publisher/Gwo/public/testy%20fizyka_1%20demo.pdf

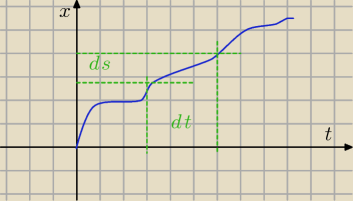
aniabb: v=ds/dt

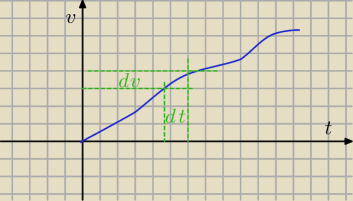
aniabb: a=dv/dt

aniabb: oczywiście na rysunkach Δ zamiast d ale nie chciało się napisać

asdf: Nie rozumiem tego kompletnie, pierw zrobię proste przykłady...

aniabb: zobacz na wzory jak mnożysz razy czas to pole jak dzielisz przez czas to przyrosty

asdf: Podstawy pierw muszę ogarnąc prędkość − przemieszczenie po czasie Na przykład: pójdę do sklepu z V = 3cm/s, będę wracał ze średnią prędkością 30mm/s To moje przemieszczenie = 0 tak?

Piotr: sorry, ze sie wcinam ale widze, ze jestes. co to (... skasowałem link na żądanie firmy reprezentującej eTrapez (Jakub) ...)?

asdf: a co ma być? strona...sciagaj co chcesz.

Piotr: yyy ja tam sie nie znam ale jakos to dziwnie wyglada. jakies gry tam sa. to jakis serwer czy jak ?

asdf: Nie wiem, ja tylko z tamtad sciagalem etrapez: (... skasowałem link na żądanie firmy reprezentującej eTrapez (Jakub) ...) To nie jest moja strona Mam inną

Piotr: nie, no linku nie potrzebuje. sam sobie wszedlem. mam wrazenie, ze to jest czyjs dysk... jak Ty to znalazles

asdf: dostałem Czemu tak drążysz ten temat?

Piotr: masz swoja strone internetowa

asdf: ze 3 lata temu dla nauczenia sie troche php zrobilem, przy okazji nauczylem sie (bardzo) duzo z css i html

Piotr: z ciekawosci ja pamietam jak kiedys szukalem etrapez to nie bylo latwo a tu wszystko szybko ze strony

asdf: @aniabb, dziękuję za pomoc, już coś mi powoli świta w głowie, jutro spróbuję to dokończyć i lepiej ogarnąć.

Piotr: od razu widac, ze kibic barcelony i manchesteru city

asdf: ja? czemu?

Piotr: mam dobra pamiec

asdf: nie mówię, że nie...ale w jaki sposób to wywnioskowałeś?

Piotr: pamietam co pisales ........... ze mna

asdf: Ja muszę spadać, bo czas goni.. P.S Zobacz sobie na meczyki.pl − ciekawe mecze jutro (ale nie dla mnie) Dobranoc!

Piotr: przypomnij sobie a nie szukaj. to by bylo za proste

Piotr: eee wole sopcast albo streamTorrent. spokojnej !