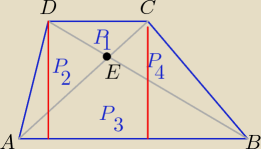
pilne,matematyka Turisas666: Przekątne trapezu podzieliły trapez na cztery trójkąty. Niech P1, P2, P3, P4 oznaczają pola tych trójkątów (rysunek obok). Wiadomo, że stosunek długości podstaw trapezu jest równy 3 : 1. Wówczas: a) P2 = P4 b) P3 = 3P1 c) P3 = 4P1 d) P3 = 6P1. http://www.voila.pl/380/vpomq/index.php?get=1&f=1

Turisas666: 2. Na rysunku obok kąt ostry trapezu prostokątnego ma miarę 60. Prosta k jest prostopadła do podstaw trapezu, zaś prosta l jest równoległa do dłuższego ramienia. Ponadto |AB| = |CD|. Niech P1 i P2 oznaczają pola figur odciętych z trapezu przez te proste. Wówczas: a) P1 < P2 b) P1 = P2 c) P1 = P2 d) P1 = P2. http://www.voila.pl/380/vpomq/index.php?get=1&f=1

Turisas666: http://www.voila.pl/380/vpomq/index.php?get=1&f=1

Turisas666:

Eta: odp: a) bo: P₂+P₃= P₃+P₄⇒ P₂=P₄

Eta: dodatkowe wyjaśnienie P(ΔABD)= P(ΔABC) ,bo mają wspólną podstawę i wysokość

Eta: Pozostałe odp: odpadają ,bo skala podobieństwa ΔABE i DCE k=3

	P3
to:		= k2=9 ⇒ P3= 9*P1 −−− takiej odp: nie ma w tych propozycjach
	P1

Turisas666: dzieki

Eta: Na zdrowie