algerba, okrąg student: Witam Środkiem cięciwy okręgu (x − 2)² + (y − 4)² = 25 jest początek układu współrzędnych. Wyznaczyć równanie prostej zawierającej tę cięciwę. Odpowiedź: x + 2y = 0. Potrzebuje pomocy w rozwiązaniu tego zadania bo już nie mam pojęcia jak to zrobić.

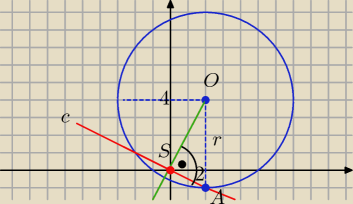
Eta: O(2,4) |OA|=r=5 to: A(2,−1) S(0,0) prosta OS ⊥ prostej AS (c −−− zawiera cięciwę

	1
pr,OS: y= 2x to pr. c: y= −		(x−xA)+yA
	2

	1
c: y= −		x lub w postaci ogólnej: c: x+2y=0
	2

ewa: Środek okręgu (2,4) r=5 Wyznaczymy równanie symetralnej tej cięciwy (będzie ona przechodziła przez (0,0) i (2,4) sym: y=ax+b 0=a*0+b 4=2a+b a=2 b=0 sym: y=2x Nasza cięciwa będzie do tej symetralnej prostopadła zatem jej wspólczynnik kierunkowy musi

	1
wynosić a'=−
	2

	1
cięciwa: y=−		x+b' i przechodzi przez (0,0) zatem b'=0
	2

	1
cięciwa: y=−		x co po przekształceniu można zapisać :
	2

2y=−x czyli x+2y=0

Eta:

student: dzięki wielkie, nie rozumiem tylko jak znalazłeś punkt A. z równania na długość odcinka OA ?