parametry aska: dla jakich wartości parametru m dziedziną funkcji y=f(x) jest zbiór wszystkich liczb rzeczywistych : f(x)=√x²−mx+m+3

aska: ?

ICSP: czyli x² − mx + m + 3 ≥ 0 − dla każdej liczby rzeczywistej zatem wystarczy aby : Δ ≤ 0

aska: a mozesz mi to rozpisac dalej prosze

rozwiązanie: D: x²−mx+m+3>0 x∊R Δ=m²−4m−12 Δ<0 m²−4m−12<0 Δm=16+48=64 m₁=−2 m₂=6 m∊(−2,6)

rozwiązanie: musi być ostro większa, nie większa równa.

aska: i nie rozumiem czemu delta jest mniejsza LUB RÓWNA zero. Anie samo "mniejsza"

ICSP: a dlaczego nie może być równa ? Według Ciebie nie istnieje pierwiastek z 0 ?

rozwiązanie: tfu... mniejsza

rozwiązanie: Chodziło mi że delta równania z m musi być ostro mniejsza, żeby nie było żadnego pierwiastka

aska: ICSP, JEŚLI MOGŁBYS/AŚ mi to przedstawić na osi i wytłumaczyć czemu z deltą jest takie założenie

ICSP: dobrze Weźmy więc m = −2 . Według ciebie nie należy ono do rozwiązań. Wstawię je do funkcji i sprawdzę co otrzymam : √x² + 2x + 1 = √(x+1)² pytam teraz jaki x mogę wstawić pod pierwiastek aby miał on sens ? Czyli (x+1)² może być ujemne Odp to nie. Tak wiec dla m = −2 dziedzina równania są wszystkie liczby rzeczywiste. Tak samo jest dla m = 6

aska: z pierwszego założenia czyli tego że to pod pierwiastkiem jest równe lub większe zero wychodzi mi : że delta jest równa m²−4m−12. i nie wiem dalej co z tym zrobić.

aska: teraz to bym policzyla miejsca zerowe a potem porównała z tym że x²−mx+m+3≥0

ICSP: ja jak na razie czekam na odpowiedź kolegi

aska: ICSP, WIADomo że masz racje tylko ja chyba teraz głupotami strzelam

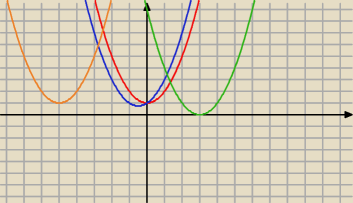
ICSP: f(x) = √x² + mx + m + 3 Dziedziną mają byc wszystkie liczby rzeczywiste więc dla dowolnego m ma zachodzić : x² + mx + m+3 ≥ 0 teraz zastanawiamy się kiedy wartości funkcji kwadratowej są ZAWSZE ≥ 0 . Otóż narysowałem ci kilka funkcji kwadratowych których wartości są zawsze ≥ 0 . Mają one następujące własności : 1^o ramiona skierowane w górę − współczynnik a > 0 2^o brak dwóch miejsc zerowych − jedno może być. czyli Δ ≤ 0 Dla funkcji : x² + mx + m + 3 masz wiec dwa warunki : 1^o a > 0 − spełniony 2^o Δ ≤ 0 ⇒ m ∊ <−2;6>

aska: czyli gdy wyliczam x²+mx+m+3≥0 to w tym momnecie wychodzi mi zbiór wartości ?

aska: yyy raczej dziedzina, sorki ?

ICSP: x² + mx + m + 3 ≥ 0

aska: kurcze. przepraszam ale nie rozumiem czemu zbiór wartości mussi być większy lub równy zero

ICSP: to spróbujmy tak pomyśleć : Co by było gdyby zbiór wartości byłby również ujemny

aska: ja bym odpowiedziała tak, że nie może być ujemny bo licz pod pierwiastkiem nie może być ujemna. Wiesz, to jest najgorsze, że mam braki w rozróżnianiu i obliczaniu wartości funkcji i dziedziny. czy możesz mi to jeszcze raz wytłumaczyc jak to rozróżnić ?

ICSP: Jeszcze raz po kolei : mamy funkcję : √x² + mx + m + 3 i mamy znaleźć taki m dla którego Dziedziną funkcji będzie zbiór liczb rzeczywistych . Czyli dla każdego x ∊ R wyrażenie x² + mx + m+3 ma być > 0 weźmy więc kilka m i zobaczmy co się będzie działo Na początek m = − 3 mam x² − 3x + 0 x² − 3x. Teraz pytam: czy dla każdego x mam że x² − 3x przyjmuje wartości wyłącznie dodatnie ? Odp to nie : x² − 3x > 0 ⇒ x(x−3) ≥ 0 ⇒ x ∊ (−∞ ; 0> suma <3 ; + ∞) tak więc dla m = −3 dziedziną funkcji jest zbiór : x ∊ (−∞ ; 0> suma <3 ; + ∞) weźmy teraz m = 0 mam : x² + 3 − x² + 3 > 0 dla każdej liczby rzeczywistej x (zauważ że x² + 3 nie posiada miejsc zerowych) weźmy ostanie m = 10 x² + 10x + 13 > 0 ale już sprawdzając dla x = −2 : 4 − 20 + 13 > 0 −3 > 0 − mamy sprzeczność. Jaki z tego wniosek ? x² + mx + m + 3 ≥ 0 przypominam że szukamy m a więc będziemy rozwiązywać nierówność ze względu na x a = 1 b = m c = m + 3 − nasze współczynniki trójmianu ax² + bx + c Z trzech wcześniejszych przykładów można było zauważyć ze gdy tylko istniały dwa pierwiastki to parabola od razu wchodziła na wartości ujemne i mieliśmy : √liczba ujemna − nie istnieje w zbiorze liczb rzeczywistych. Wystarczy wiec wyeliminować to "wchodzenie" na liczby ujemne poprzez albo nie dotykanie osi OX − brak pierwiastków albo odbijanie od osi OX − jeden pierwiastek. Co decyduje o ilości pierwiastków w równaniu kwadratowym Oczywiście delta, więc otrzymujemy że nasza Δ musi być albo < 0 − brak pierwiastków albo = 0 − jeden pierwiastek. Co jako jeden warunek możemy zapisać Δ ≤ 0

aska: O jejku , ICSP, ALE SIĘ napisałeś. ale wielkie dzięki, w końcu zrozumiałam ! Jeszcze raz− DZIĘKUJĘ