Elipsa qaz: Dane A(1,1) E: 4x²+9y²−36=0 B₁C ∊E,B=S_A(C) Szukane:l−prosta A,B,C∊l

qaz: ?

qaz:

qaz: ?

aniabb: jak dla mnie za duże skróty myślowe

qaz: No właśnie.Sam nie wiem o co w tych kompletnie chodzi

Mila: 4x²+9y²−36=0 /:36

x2		y2
	+		=1 elipsa
9		4

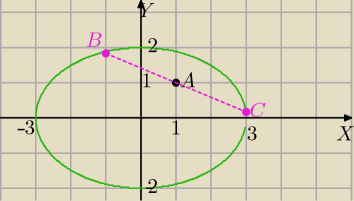
x=0 to y=2 lub y=−2 y=0 to x=3 lub x=−3 Punkt C jest symetryczny do punktu B względem p.A i B oraz C należą do elipsy Punkt A=(1;1) jest środkiem odcinka BC

b1+c1		b2+c2
	=1 i		=1⇔b1+c1=2 i b2+c2=2
2		2

oraz współrzędne punktów B i C spełniają równanie elipsy. ułóż jeszcze dwa równania i dokończ.