Wielomiany PuRXUTM: Wyznacz wszystkie wartości parametru m, dla których wielomian W(x)=(m+3)x⁴−2mx²+m−1 ma dokładnie dwa pierwiastki

Saizou : x²=t W(x)=(m+3)t²−2mt+m−1 Δ≥0 t₁*t₂<0 m+3≠0 czy jakoś tak

PuRXUTM: aha rozumiem t₁*t²<0 żeby jedno t było mniejsze od zera wtedy nie spełnia założenia i zostaje tylko jedno t z którego mamy 2 pierwiastki. Dzięki

Saizou : tak

TriviaI: 1. Załóż, że m = −3 i zobacz czy powstały wielomian ma dokładnie dwa pierwiastki. 2. Rozważ przypadek m ≠ −3 oraz zrób podstawienie u = x². Wtedy (m+3)u² − 2mu + (m−1) = 0 3. Chcemy mieć albo dwa pierwiastki u₁,u₂ o różnych znakach, albo jeden pierwiastek u₀ > 0. Wydaje mi się, że to powinno wystarczyć.

Saizou : witaj Trivial fakt zapomniałem o przypadku gdzie m=−3

PuRXUTM: dzięki Trivial

TriviaI: cześć Saizou. ;>

PuRXUTM: Chcemy mieć albo dwa pierwiastki u1,u2 o różnych znakach, albo jeden pierwiastek u0 > 0. mam mieć założenia z delty i tych miejsc zerowych. Tylko tutaj mam mieć sumę czy część wspólną bo nie ogarniam

TriviaI: u₁, u₂ o różnych znakach: 1. Δ_u > 0, 2. u₁u₂ < 0 u₀ > 0 − jedyny pierwiastek: 1. Δ_u = 0 2. u₀ + u₀ > 0 ← ukryty wzór Viete'a na sumę pierwiastków.

TriviaI: I na koniec dajesz sumę zbiorów.

PuRXUTM: a dla Δ_u>0 daję część wspólną ?

TriviaI: (Δ_u > 0 ∧ u₁u₂ < 0) ∨ (Δ_u = 0 ∧ u₀+u₀ > 0)

Saizou : a nie można tego załatwić zapisem u₁*u₂<0 Δ≥0

PuRXUTM: dzięki

TriviaI: Jeśli u₁ = u₂ = u₀ to mamy: u₀*u₀ = u₀² < 0 → w ogóle ten warunek nic nie daje.

PuRXUTM:

	3
Wyszło mi m∊<−3;1) U {		} mógłby ktoś sprawdzić ? Bo w odpowiedziach jest
	2

	6
m∊(1;		)U(2;3)
	5

I mam jeszcze pytanie dlaczego można zastosować ten " ukryty " wzór Viete'a

PuRXUTM: help

Eta: Dzisiaj już nie mam siły, oczy mam już za bardzo zmęczone i muszę nieco odpocząć Jutro sprawdzę ... ok?

Saizou : x²=t t≥0 W(x)=(m+3)t²−2mt+m−1 − dla m=−3 (−3+3)t²−2*(−3)t−3−1=0 6t−4=0 6t=4

	2
t=
	3

	2
x2=
	3

	√6		√6
x=		lub x=−
	3		3

− dla m≠3 a) t₁ i t₂ są różnych znaków Δ>0 4m²−4(m+3)(m−1)>0 4m²−4(m²+2m−3)>0 4m²−4m²−8m+12>0 −8m>−12

	3
m<
	2

t₁*t₂<0

m−1
	<0 /(m+3)2
m+3

(m+3)(m−1)<0 m∊(−3:1) b) dla t₁=t₂≠0 Δ=0

	3
m=
	2

(1,5+3)t²−2*1,5t+1,5−1=0 4,5t²−3t−0,5=0

	3		1
to=		=
	9		3

zatem m∊<−3:1) ∪ {³₂} czyli dobrze rozwiązałeś i musi być błąd w książce

PuRXUTM: Dzięki wielkie Saizou !

Saizou : ja nawet sprawdzałem w geogebrze

PuRXUTM: co to jest geogebra ?

Piotr: http://www.geogebra.org/webstart/geogebra.html

PuRXUTM: dzięki

TriviaI: http://www.wolframalpha.com/input/?i=plot+%28m%2B3%29x^4%E2%88%922mx^2%2Bm%E2%88%921+%3D+0+from+m+%3D-7+to+2%2C+x%3D-5+to+5 Można odczytać z wykresu gdzie oś 'x' przecina oś 'm' dokładnie 2 razy.

PuRXUTM: nie za bardzo wiem jak to odczytać

TriviaI: Kiedy prosta m = c (na wykresie pionowa), gdzie c jest jakąś stałą przecina wykres dokładnie w dwóch miejscach? Odpowiedź: mniej więcej dla c∊[−3,1)u{3/2}. W ten sposób możesz sprawdzić swój wynik − pasuje on do tego co widać na wykresie.

PuRXUTM: dalej nie ogarnia gdzie jest c

TriviaI: Zaraz to narysuję...

Saizou : według mnie łatwiej wbić do geogebry formułkę

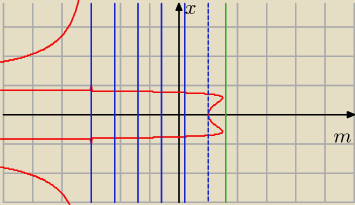
TriviaI: Narysowałem kilka prostych m=c (na niebiesko i zielono)

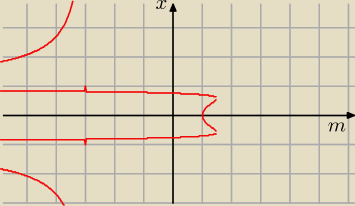
TriviaI: Wykres narysowany jeszcze raz, żeby nie zaciemniać.

PuRXUTM: dzięki