objętość, pole całkowite i pole przekroju walca. ona: CZY TO JEST ROZWIĄZANE POPRAWNIE? Po rozwinięciu powierzchni bocznej walca otrzymamy prostokąt, którego jeden z boków jest 3 razy dłuższy od drugiego i kwadrat jego przekątnej wynosi 160. Przyjmując, że krótszy z boków prostokąta jest wysokością walca, oblicz: pole całkowite walca, objętość walca, pole przekroju walca. powstaje trójkąt prostokątny o bokach c²=160 h 3h=L i z twierdzenia Pitagorasa wyliczam, że h=4 czyli L=3*4=12 L=2πR=12 więc R=⁶_π (?) Pc=2πR²+2πRh z czego wychodzi Pc=³⁶⁰_π V=π*(⁶_π)²*4=¹⁴⁴_π Pprz=2*⁶_π*4=⁴⁸_π (?)

Mati_gg9225535:

	6		6		36		72
Pc = 2πR2+2πRh = 2π (		)2 + 2π (		) * 4 = 2*		+ 12*4 =		+48=
	π		π		π		π

	24(3+2π)
=
	π

Mati_gg9225535:

	36		144
V=		* 4 =
	π2		π2

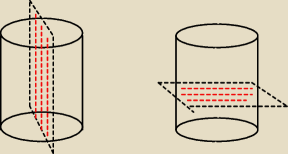
Mati_gg9225535: ten przekrój to ma być w pionie czy w poziomie ?

Eta: Pomyłka w P_c , reszta ok popraw P_c= 2πr(r+h)=........

Mati_gg9225535:

Eta: Może miało być : pole przekroju osiowego walca?

Mati_gg9225535: może

ona: tak, pole przekroju osiowego przepraszam

ona: już widzę błąd, dziękuję za pomoc wszystkim.

Eta: