planimetria Nutka: Treść zadania: długość ramion a i b trapezu są równe odpowiednio 5 cm i 3 cm. Odcinek łączący środki tych ramion dzieli trapez na dwie równe części w ten sposób, że stosunek ich pól jest równy 5:11. oblicz pole trapezu wiedząc, że można wpisać w niego okrąg. Bardzo potrzebuję tego rozwiązania......

Artur_z_miasta_Neptuna: odcinek łączący środki ramion oznaczmy jako e d (dłuższa),c (krótsza) to podstawy trapezu

	d+c
e =
	2

H −−− wysokość trapezu h₁,h₂ −−− wysokości dolnej i górnej części trapezu

	1
h1=h2 =		H
	2

Pgorny trapez		5
	=
Pdolny trapez		11

stąd wynika, że:

	d + e		c+e
5*		*h1 = 11*		*h2
	2		2

czyli: 5(d+e) = 11(c+e)

	c+d		c+d
5d + 5		= 11c + 11
	2		2

10d + 5c + 5d = 22c + 11c + 11d 4d = 28c d = 7c czyli trapez ma boki o długości: c cm, 7c cm, 5 cm i 3 cm skoro można wpisać w ten trapez okrąg, to można zastosować tw. o stosunku boków czworokąta opisanego na okręgu: a+b = c+d 3+5 = c + 7c 8 = 8c c=1 d=7c = 7 wprowadzamy dwie nowe niewiadome: x, y (części dolnej podstawy) x² + H² = 5² y² + H² = 3² x+y = 7−1 otrzymujesz układ trzech równań z trzema niewiadomymi −−− rozwiąż. Masz już wszystkie dane potrzebne do wyliczenia pola tegoż trapezu ... obliczasz i koniec zadania

Bogdan:

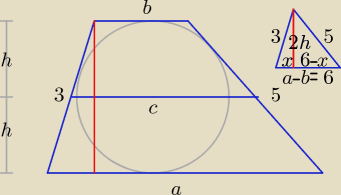
	a + b
a + b = 3 + 5 ⇒ a + b = 8 ⇒ c =		= 4 i b = 8 − a
	2

a + c   *h 2		11		a + 4		11
	=		⇒		=		⇒ a = 7
c + b   *h 2		5		8 − a + 4		5

b = 8 − 7 = 1 (2h)² + x² = 9 ⇒ 4h² + x² = 9 (*)

	5
(6−x)2 + (2h)2 = 25 ⇒ 36−12x+x2+4h2 = 25 ⇒ 36 − 12x + 9 = 25 ⇒ x =
	3

	25		14
(*) 4h2 +		= 9 ⇒ h2 =		i h > 0 ⇒ h = ...
	9		9

	a + b
Pole trapezu P =		* h = 4 * h = ...
	2

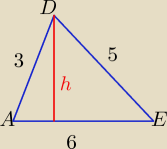Eta: Długość h można też wyliczyć ze wzoru Herona dla Δ AED

	a+b+c
P= √p(p−a)(p−b)(p−c) , p=
	2

p= 2 P= √7*4*2*1= 2√14 i P= 3h to :

	2√14
h =
	3

	a+b
P(trapezu)=		*h= 4h= .........
	2