Wykaż, że zachodzą poniższe równości.

Wykaż, że zachodzą poniższe równości. CryGirl :(: Witam! Proszę o pomoc w pewnym przykładzie. Jak wykazać, że: ∩ a) (A ∪ B) \ A = B \ (A ∩ B) − nic nie wychodzi

b) A ∪ (B \ C) = [(A ∪ B) \ C] ∪ (A ∩ C) − tutaj zatrzymuje się w pewnym momencie i nie wiem jak dalej

c) A x (B \ C) = (A x B) \ (A x C) − tutaj coś z iloczynu kartezjańskiego, którego nie potrafię zrobić

Jak ktoś potrafi to zrobić to bardzo proszę o pomoc

Po prostu nie jestem w stanie tego udowodnić

31 paź 23:20

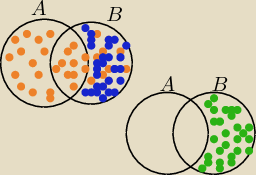
aniabb: rysunek

31 paź 23:25

CryGirl :(: A jak to udowodnić pisemnie?

31 paź 23:28

aniabb: diagramy Venna też są metodą emotka

31 paź 23:30

CryGirl :(: I na I roku studiów to przejdzie ?!

31 paź 23:33

aniabb: x∊A∪B/A ⇔ x∊A ⋁ x∊B ⋀ x∉A ⇔ x∊B ⋀ x∉A ⇔ x∊B ⋀ x∉ A∩B ⇔ x∊B/ A∩B

31 paź 23:34

aniabb: a było w treści zadania jaką metodą?

31 paź 23:34

CryGirl :(: Tak wykorzystując prawa rachunku zbiorów oraz definicję iloczynu kartezjańskiego rozwiąż:...

31 paź 23:36

aniabb: no to tak jak 23:34

31 paź 23:39

kambik: b) P=[(A ∪ B) \ C] ∪ (A ∩ C) = [(A ∪ B)∩ C`] ∪ (A ∩ C)=(A∩ C`) ∪ (B∩C`) ∪ (A ∩ C)= a (A∩ C`) ∪(A ∩ C)=A więc =A ∪ (B∩C`)=A ∪ (B\C)=L

31 paź 23:51

CryGirl :(: A ten iloczyn kartezjański? Jak to zrobić?

1 lis 00:03