zadania
zadanie: trapez rownoramienny o podstawach dlugosci a i 3a obraca sie
a) dookola prostej zawierajacej krotsza podstawe
b) dookola prostej zawierajacej dluzsza podstawe. oblicz stosunk objetosci otrzymaych bryl.
moge prosic o rysunek
wiem ze w a) H=3a ; b) H=a a pozniej ?
31 paź 20:22
konrad:
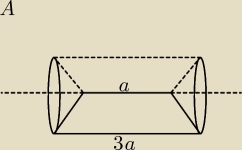
31 paź 20:30
konrad:
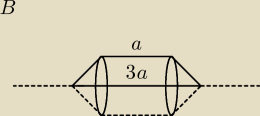
31 paź 20:32
konrad: | | 1 | | 3a−a | |
a) Va=πr2*3a*−2* |
| πr2*( |
| ) |
| | 3 | | 2 | |
| | 1 | | 3a−a | |
b) Vb=πr2*a+2* |
| *πr2*( |
| ) |
| | 3 | | 2 | |
| | Va | |
uprość sobie te wzory, a potem policz |
| albo na odwrót |
| | Vb | |
31 paź 20:36
zadanie: w a) wysokosc stozka jest rowna a (bo tak widac na rysunku 3a=a+a+a) ; a promien stozka to h
(wysokosc) trapezu rownoramiennego i walca
w b) tez tak

i co dalej jak obliczyc objestowsc stozka i co pozniej z nia zrobic?
31 paź 20:43
31 paź 20:47
konrad: już napisałem
31 paź 20:47
konrad: | | 3a−a | |
to |
| to jest wysokość stożka |
| | 2 | |
31 paź 20:48


 i co dalej jak obliczyc objestowsc stozka i co pozniej z nia zrobic?
i co dalej jak obliczyc objestowsc stozka i co pozniej z nia zrobic?