Określić parzystość/nieparzystość funkcji bartekcmg: f(x)= ( e^2x + e^−2x ) tgx na początek jak w ogóle określić dziedzinę takiej funkcji ?

aniabb: dziedzina tg

bartekcmg: czyli D;R ... czyli tego co w nawiasie nie biorę pod uwagę? potem mam taki przykład i też nie wiem jaka dziedzina: f(x)=cos1/4 x − tg²x

Bogdan: Nie, D ≠ R

Mila: 1) e²x i e^−2x to działania wykonalne, dodawanie też

	π
tgx nie istnieje dla x=		+kπ
	2

	π
D=R\{		+kπ } gdzie k∊C
	2

2) dziedziną cosinusa jest R, ale tgx , jak wyżej.

bartekcmg: mam jeszcze taki przykład: f(x)=π−2arccosx . Tutaj chodzi mi po głowie ten wzór na wartości ujemne dla arccosx, ale nie wiem czy to właściwy trop

bartekcmg: bardzo proszę o wskazówki

Mila: Jakie masz polecenie do tej funkcji?

bartekcmg: czy funkcja jest parzysta czy też nieparzysta

Mila: wskazówka: arccos(−x)=π−arccosx

bartekcmg: o tym wzorze pisałem właśnie u góry czyli − ... parzysta

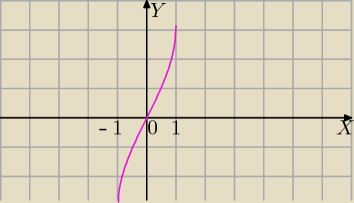
Mila: f(x)=π−2arccosx . −f(x)=−π+2arccosx f(−x)=π−2arccos(−x)=π−2(π−arccosx)=π−2π+2arccosx⇔ f(−x)=−π+2arccosx=−f(x) ⇔funkcja jest nieparzysta zobacz wykres, jest symetryczny względem punktu (0;0).

bartekcmg: w odpowiedziach mam "parzysta" ...

bartekcmg: i dlaczego ten wykres jest przeciwny do wykresu arccosx? , tzn. arccosx jest malejąca... a tutaj inaczej...

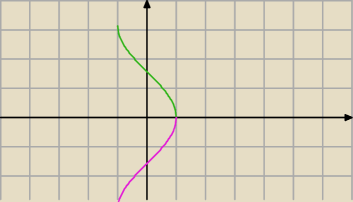
Mila: y=arccosx funkcja malejąca (zielony) y=−arccosx funkcja rosnąca (różowy) y=2x funkcja rosnąca y=−2x funkcja malejąca. Jeśli chodzi o parzystość to zobacz treść zadania, może coś zmieniłeś.

bartekcmg: dzięki za szczegółowe objaśnienia (pewnie w odpowiedziach z książki jest błąd)