pomocy :) miodzio: Rozważ zbiory {0,1} (0,1) i [0,1]. Czy następujące stwierdzenia są prawdziwe? a) {0,1}⊆(0,1) b) {0,1}∊[0,1] c) (0,1)∊[0,1] d) {0,1}∊Z e) [0,1]∊Z f) [0,1]∊Q g) 1/2 i π/4 są elementami {0,1} h) 1/2 i π/4 są elementami (0,1) i) 1/2 i π/4 są elementami [0,1]

Godzio: a) nie prawda bo {0,1} ⊆ [0,1] b) nie prawda bo musiało by być: {0,1} ∊ ( [0,1] ∪ { {0,1} } ) c) prawda d) nie prawda bo Z = { ..., −1, 0, 1, ... }, (podobnie jak w B {0,1} ∊ Z ∪ { {0,1} } e) nie prawda − oczywiste f) nie prawda g) nie prawda h) prawda i) prawda Co do " ∊ " Jeśli A ∊ B to B = { A, INNE ELEMENTY } Natomiast "⊆" A ⊆ B to znaczy, że każdy ELEMENT zbioru A jest elementem zbioru B. A = {1,2,3} i B = {1,2,3,4} to A ⊆ B

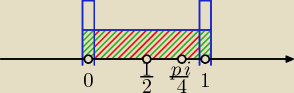
Bogdan: {0, 1} − zbiór dwuelementowy złożony z liczb 0 i 1 (na rysunku słupki); (0, 1) − zbiór wszystkich liczb rzeczywistych od 0 do 1 wyłącznie, czyli bez 0 i bez 1, przedział otwarty dwustronnie od 0 do 1 (na rysunku zaznaczony na czerwono); [0, 1] − zbiór wszystkich liczb rzeczywistych od 0 do 1 włącznie, czyli z 0 i z 1, przedział domknięty (zamknięty) od 0 do 1, w ostatnim czasie oznaczany <0, 1> (na rysunku zaznaczony zielonym kolorem); ℤ − zbiór liczb całkowitych; ℚ − zbiór liczb wymiernych. a) nie b) tak, przy czym zapis powinien być taki: {0, 1}⊂[0, 1] albo {0, 1}⊂<0, 1> c) tak, przy czym zapis powinien być taki: (0, 1)⊂[0, 1] albo (0, 1)⊂<0, 1> Spróbuj dalej samodzielnie

Bogdan: b) i d): prawda czy nieprawda?

miodzio: no dobra ale czym rożni się znak ⊂ od ⊆ wiem, że ten pierwszy to np a jest podzbiorem b czyli każdy element a należy do b a o co chodzi w tym ⊆?

Bogdan: A⊂B zbiór A zawiera się w zbiorze B, np. {1, 2, 3,}⊂{0, 1, 2, 3, 4}, A⊆B zbiór A zawiera się w zbiorze B lub zbiory A i B są równe, np.: {1, 2, 3}⊆{0, 1, 2, 3, 4}, {1, 2, 3}⊆{1, 2, 3} Symbol ⊆ jest wg mnie nadinterpretacją, bo np.: {1, 2, 3}⊂{1, 2, 3}, zbiór pełny jest przecież także swoim podzbiorem. A jakie jest zdanie innych forumowiczów w tej sprawie?

miodzio: też tak myślę ... zatem moim zdaniem a) nie b) tak c)tak d) tak e) tak f) nie g) nie h) tak i) tak .. zgadza się bogdan ?

Bogdan: Sprawdź e),

Godzio: Ale jeżeli było tam "∊" to powinniśmy to traktować jako "należenie" a nie "zawieranie". Tak mi się wydaję przynajmniej.

Bogdan: Zapis {0, 1} oznacza zbiór, można zapisać: 0∊[0, 1], 1∊[0, 1], {0, 1}⊂[0, 1]

Godzio: Wiem wiem, ale zbiór też może należeć do innego zbioru.

Bogdan: Myślę, że miodzio błędnie użył znak ∊

miodzio: a no faktycznie. Bo ja to potraktowałem tak, że skoro jest znak ∊ to wystarczy, że jakikolwiek element zbioru [0,1] ma należeć do Z a to trzeba traktować jako całość ? czyli każdy element zbioru [0,1] należy do Z ? bo jak tak to e oczywiście nie

miodzio: no i sam się zaplątałem ..

miodzio: czyli e to prawda ?

Bogdan: Zbiory zawierają się w sobie. W mowie potocznej, ale nie w języku matematyki, używa się powszechnie określenia " należy", stąd jak sądzę jest silna chęć do używania znaku ∊ w każdej sytuacji. Rozróżnia się wyraźnie znaki: ∊ oraz ⊂.

Godzio: ∊ − całość ⊆ − elementy

miodzio: aj nie ...... XD dobrze mówiłem XD

Bogdan: e) cały przedział [0, 1] ⊄ ℤ, czyli nie zawiera się w ℤ

miodzio: czyli a) nie b) tak c) tak d) tak e) nie f) nie g)nie h) tak i) tak

Godzio: Bogdan, miałem to jakieś 2 wykłady wcześniej na wstępie do matematyki, i z tego co się dowiedziałem to zbiory mogą należeć do innych zbiorów lub zawierać się w sobie. Np. Zbiór {1,2,3} należy do zbioru: {1,2, {1,2,3}, 4}, albo zawiera się w zbiorze: {1,2,3,4}. {1,2,3} ∊ {1,2, {1,2,3}, 4} {1,2,3} ⊆ {1,2,3,4}

Bogdan: Wg mnie teraz jest miodzio dobrze

miodzio: dobra dzięki za pomoc Panowie

Bogdan: Jeśli {1, 2, 3} traktujemy jako element zbioru {1, 2, {1, 2, 3}}, to znak ∊ jest uzasadniony, ale podkreślam, że {1, 2, 3} jest w tym przypadku pojedynczym obiektem, elementem. Znak ∊ stosujemy między elementem zbioru i zbiorem, do którego należy. Wyrażenia {1, 2}, (1, 2), [1, 2] zdefiniowałem na początku jako zbiory i przy takim ujęciu właściwy jest znak ⊂ między nimi.

Godzio: Ok. Rozumiem

Bogdan: Interesująca dyskusja przy okazji tego zadanka się wywiązała. Takie rozważanie problemów jest bardzo pouczające nawet dla wytrawnych znawców określonej dziedziny. Myślę, że jednym z motorów postępu i rozwoju, również swojego, jest umiejętność wątpienia i szukania odpowiedzi na pojawiające się wątpliwości.

Godzio: W pełni się z tym zgodzę

aniabb: i standardowa kość niezgody z ważniaka Czy zbiór bocianów jest elementem zbioru wszystkich ptaków?

Marta : Proszę o wytłumaczenie zadania rozważ zbiory. Skąd mam wiedzieć czy stwierdzenie jest prawdziwe? A {0, 1} ⊆ (0,1) B {0,1} ∊ [0,1] C (0,1) ⊆ [0,1] D (0,1) ⊆ (0,1) E {0,1} ⊆ Z F [0,1] ⊆ Z G (0,1) ⊆ Z

Adamm: gotowca szukasz?

Marta : Mam to rozwiązane bo robiliśmy to na studiach na zajęciach. Niestety wykładowca to nie umie tłumaczyć. A takie zadanie będzie na zaliczenie. Ja chce tylko to zrozumieć. Ja nie wiem o co w tym chodzi. Na dowód że nie kłamie wysyłam odpowiedzi spisane z prezentacji na wykładzie. A Nie B Nie zdążyłam spisać C Tak D Nie zdążyłam spisać E Tak F Nie B i D było na końcu zadania. Błagam o wytłumaczenie mi jak się rozwiązuje takie zadania.

Adamm: a wiesz co to znaczy A⊆B jeśli A i B to zbiory?

Marta : Zapomniałam rozważ zbiory {0,1}, [0,1], (0,1) A {0, 1} ⊆ (0,1) B {0,1} ∊ [0,1] C (0,1) ⊆ [0,1] D (0,1) ⊆ (0,1) E {0,1} ⊆ Z F [0,1] ⊆ Z G (0,1) ⊆ Z

Marta : Nie wiem

Marta : Zbiór A jest podzbiorem B?

Adamm: A⊆B znaczy że dla dowolnego x, x∊A to x∊B. {0, 1} to zbiór złożony z 0 i 1 (0, 1) to zbiór złożony z liczb rzeczywistych x, 0<x<1 [0, 1] to zbiór złożony z liczb rzeczywistych x, 0≤x≤1 Z to zbiór liczb całkowitych (Zahl z niemieckiego)

Marta : Nadal nic mi to nie mówi. Powiesz mi dlaczego {0, 1} ⊆ (0,1) jest nie prawdziwym stwierdzeniem?

Adamm: x∊{0, 1}, czy wtedy x∊(0, 1)?

Marta : Szukałam w internecie ale nic nie znalazłam. Błagam o pomoc.

Marta : Różni się tylko nawiasami ten po prawej ma ( ) a po lewej {}. Nadal nie wiem o co chodzi.

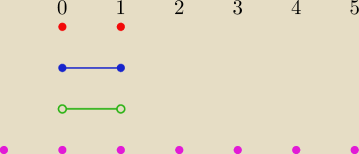
Adamm: czerwone − {0, 1} niebieskie − [0, 1] zielone − (0, 1) fioletowe − Z

Marta : {0,1} nie ma kreski (0,1) ma kreski Czyli nie są takie same. To dlatego stwierdzenie jest nie prawdziwe?

Adamm: mi się nie chce tłumaczyć jak krowie na rowie, albo pomyślisz i zrozumiesz, lub po prostu nie zdasz i będziesz poprawiać

Adamm: najlepiej to pójdź do niego na konsultacje

Marta : Wytłumacz mi błagam bo nigdy nie zdam. Naprawdę nie wiem o co chodzi w tym zadaniu. Nie możesz odpowiedzieć na pytanie dlaczego {0, 1} ⊆ (0,1) jest nie prawdziwymstwierdzeniem?

Marta : On nie umie tłumaczyć. Byłam

Marta : Błagam pomóż mi. Jestem niepełnosprawna.

Pytający: • x∊{0, 1} ⇔ (x=0 ∨ x=1) • x∊(0,1) ⇔ (0<x<1) • {0, 1} ⊆ (0,1) ⇔ (dla każdego x∊{0, 1} zachodzi x∊(0,1)) co oczywiście nie zachodzi (nie jest to prawdziwym stwierdzeniem), bo 0∊{0, 1}, ale 0∉(0,1)