a aga: w trapezie rownoramiennym o przekatnej 13cm można wpisać okrąg. odcinek łączący srodki ramion trapezu ma dlug. 12. oblicz długość ramion i pole trapezu

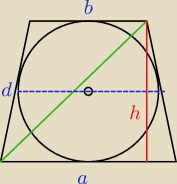
Tad: jeśli w trapez można wpisać okrąg to ... d=12 h policzysz pole też −)

Artur_z_miasta_Neptuna: Tad − to ciekawa ciekawość ... patrz chociażby Twój rysunek −−− za nic promień okręgu NIE JEST

	12
równy		= 6
	2

Artur_z_miasta_Neptuna:

a+b
	= 12
2

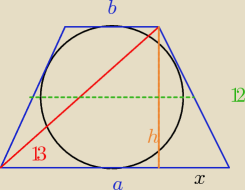
a−x = b+x

a+b		(a−x) + (b+x)
	=		... czyli (a−x) = (b+x) = 12
2		2

(a−x)² + h² = 13² 12² + h² = 13² h² = 169 − 144 h² = 25 h=5

	a+b
Ptrapezu =		*h = 12*5 = 60
	2

ramiona: korzystasz z twierdzenia o długości boków czworokąta opisanego na okręgu. a+b = c+d ... gdzie c,d ramiona trapezu 24 = c+d a przeciez jest to trapez równoramienny, więc c=d 24 = 2c c = 12

Tad: a+b=2d

a+b
	=d
2

	a+b
... a czym jest odcinek łączący środki ramion ? nie
	2

... pisałem coś o promieniu okręgu?

Tad: ... ot i ciekawa ciekawość −

Artur_z_miasta_Neptuna: wybacz ... zasugerowałem się oznaczeniem 'd' jako średnica okręgu

Tad: −