Oblicz dla jakich wartości parametru m okregi xyz: Oblicz dla jakich wartości parametru m okręgi o równaniach (x−m)²+(y+4)²=8 (x−2)²+(y+m)²=2 a) styczne wewnętrznie r₁=2 √2, S₁=(m, −4) r₂=√2, S₂=(2, −m) A wiec liczę: |r1r2|= √2m²+4m+20 Δ < 0 A wiec gdzie jest błąd?

Ann: bo tu nie bedzie chodzilo o promienie bo te masz stale a o to gdzie srodki tych okregow sie znajduja

xyz: no tak ale mamy warunek |S₁S₂|<r₁−r₂

PuRXUTM: okręgi są styczne wewnętrznie jeżeli IS₁S₂I=Ir₁−r₂I i liczysz

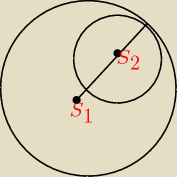
Ann: policz odleglosc S₁S₂ i beda styczne wewnetrznie gdy ta odleglosc bedzie = r₁−r₂

xyz: Czyli √2m²−12m+20=√2|*()² a=2 b=−12 c=18 Δ=80 No tak tylko w książce mam m₀ tylko.

xyz: coś jest nadal źle m₁=3−√5 m₂=3+√5 −−−−−−−−−−−−−−−−−−−−−−−−−−− według odpowiedzi: m₀=3

xyz: Wszytko ok to ja zrobiłem błąd. Dzięki za wszystkie odpowiedzi