sa jeszcze jakies pierwiastki?

sa jeszcze jakies pierwiastki? Mateush444: x⁶−3x³−5x³+15=0 x=√3 i x=−√3

30 paź 21:02

ICSP: prócz tych które są źle policzone to tak

30 paź 21:04

Mati_gg9225535: tam jest −3x³ i −5x³ ? chodzi mi o wykładniki, są takie same?

30 paź 21:05

Mateush444: tak bo tam bylo −8x³ to rozpisalem. jak obliczyc dobre?

30 paź 21:06

Mateush444: wsumie zamiast √3 powinno byc chyba √5 to samo z minusowym

30 paź 21:08

ICSP: a nie możesz podstawić t = x³ , t ∊ R i otrzymasz równanie kwadratowe emotka

30 paź 21:08

Mateush444: chyba o to nawet chodzi jak teraz patrze

jutro mam kolokwium i juz nie mysle...

30 paź 21:09

asdf: x⁶ − 8x³ + 15 = 0 t = x³

30 paź 21:10

ICSP: ale twój sposób jest również dobry emotka

Uczy myślenia a to dobrze

x⁶ − 3x³ − 5x³ + 15 = 0 (x³ − 5)(x³ − 3) = 0 x = ³√3 v x = ³√ 5

30 paź 21:10

asdf: albo tak: x⁶ − 3x³ − 5x³ + 15 = 0 x³(x³ − 3) − 5(x³ − 3) = 0 (x³ − 3)(x³ − 5) = 0 x³ = 3 x³ = 5

30 paź 21:12

Mateush444: tylko mi dziwne rzeczy wyszly

x²(x³−3)−5(x³−5)

30 paź 21:12

Mateush444: aaa... x³

30 paź 21:13

Mateush444: jesli ogarniacie dobrze matme to mialbym jeszcze kilka

30 paź 21:13

Mateush444: sin⁴x−cos⁴x=1/2

30 paź 21:15

ICSP: xD

	1
−cos2x =
	2

	1
cos2x = −
	2

30 paź 21:16

zosia: x6−3x3−5x3+15=0 x=√3 i x=−√3 x6 − 3x3 − 5x3 + 15 = 0 x3(x3 − 3) − 5(x3 − 3) = 0 (x3 − 3)(x3 − 5) = 0 x3 = 3 x3 = 5

30 paź 21:17

Mateush444: tylko ze we wzorze jest do 2 potegi a nie do 4. jak to dziala?

30 paź 21:17

asdf: sin⁴x − cos⁴x = 1/2 (sin²x + cos²x)(sin²x − cos²x) = 1/2 sin²x − cos²x = 1/2 −(cos²x − sin²x) = 1/2 −cos2x = 1/2 cos2x = −1/2 Nie wiem czy dobrze

30 paź 21:17

ICSP: tam nie ma potęgi cos2x oznacza cosinusa podwojonego kąta

30 paź 21:17

Mateush444: nie ogarne tego do jutra emotka

a juz tydzien robie te zadania...

30 paź 21:19

asdf: Tu masz taki wzór: cos(x + y) = cosxcosy − sinxsiny Dla takich samych kątów otrzymasz: cos(x + x) = cosxcosx − sinxsinx = cos²x − sin²x cos(x + x) = cos2x

30 paź 21:19

asdf: Nie poddawaj się Mateusz, nie takie rzeczy w jedną noc się ogarniało emotka

Zagrzej sobie kawy albo jak masz to weź najlepiej guarane i jazda emotka

Na pewno ktoś Ci tutaj pomoże

30 paź 21:21

Mateush444: dzieki juz wiem o co chodzi. rozwiazanie to pi+2k*pi?

30 paź 21:21

ZKS:

	1
cos(2x) = −
	2

	2		4
2x =		π + k * 2π ∨ 2x =		π + k * 2π
	3		3

	π		2
x =		+ k * π ∨ x =		π + k * π
	3		3

30 paź 21:26

asdf:

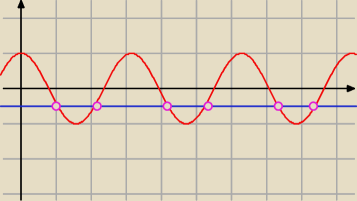
A graficznie to będzie tak wyglądać ( chyba )

30 paź 21:28

Mateush444: ctg(x)−cos(x)=^1−sin(x)_2sin(x)

30 paź 21:29

Mateush444: a ja ze 2x=−¹₂

30 paź 21:30

Mateush444: ctg trzeba rozpisac na cos/sin i wspolny miamownik no nie?

30 paź 21:30

Mateush444: to bedzie cos(x)−cos(x)*sin(x)/sin(x) chyba

30 paź 21:31

asdf:

	1 − sin(x)
ctg(x) − cos(x) =
	2sin(x)

30 paź 21:31

ZKS: Dziedzina najpierw cos(x) ≠ 0 ⇒ x ≠ ? ∧ sin(x) ≠ 0 ⇒ x ≠ ?.

30 paź 21:33

Mateush444: 0 jest w pi/2+k*pi dla cos i k*pi dla sin

30 paź 21:36

Mateush444: asdf tak jest na kartce

30 paź 21:37

ZKS: Wiec jaka jest Twoja dziedzina?

30 paź 21:38

Mateush444: http://imageshack.us/content_round.php?page=done&l=img10/6015/54117641206964526492106.jpg

30 paź 21:39

Mateush444: x nalezy do R z pominieciem k*pi/2 raczej emotka

30 paź 21:41

ZKS: W porządku to teraz rób porządek z tym równaniem.

30 paź 21:48

Mateush444:

cosx−cosx*sinx

sinx

30 paź 21:49

Mateush444: mozna obliczyc jedna strone i zobaczyc czy L=P?

30 paź 21:50

ZKS: Ale przecież to jest chyba równanie a nie tożsamość?

30 paź 21:51

Mateush444: a jak to odroznic? pisalo by udowodnij ze ....=.... ?

30 paź 21:52

ZKS: Przepraszam widziałem tam tg(x) a jest przecież ctg(x) więc dziedziną będzie samo sin(x) ≠ 0. emotka

30 paź 21:53

Mateush444: mialem sie pytac czemu i zapomnialem

30 paź 21:53

ZKS: Tak raczej by było napisane udowodnij tożsamość.

30 paź 21:54

Mateush444: bo zauwazylem to emotka

30 paź 21:54

Mateush444:

cos(x)−cos(x)*sin(x)		1 − sin(x)
	−		=0
sin(x)		2sin(x)

i teraz lewa strone *2?

30 paź 21:56

ZKS: Możemy nawet przez 2sin(x) tylko napisz dlaczego? emotka

30 paź 21:57

Mateush444: do wspolnego trzeba sprowadzic zeby licznik mozna bylo odjac tak sądzę

30 paź 21:58

Mateush444: a jak Twoim sposobem to zniknie licznik

tylko ze te pierwsze bedzie trzeba *sin(x) ? emotka

30 paź 22:00

ZKS: Ale się pytam dlaczego możemy pomnożyć od razu przez 2sin(x)?

30 paź 22:00

Mateush444: no bedzie latwiej liczyc

30 paź 22:02

Mateush444: mozna bo taki sam mianownik tylko tam z dwójką jest

30 paź 22:03

ZKS: Ale dlaczego to można zrobić? Skąd wiadomo że ten 2sin(x) jest różny od 0? emotka

30 paź 22:03

Mateush444: zalozenia robilem

30 paź 22:04

ZKS: No właśnie więc teraz ułatw sobie życie i pomnóż przez 2sin(x) aby pozbyć się mianownika. emotka

30 paź 22:06

Mateush444: 2cos(x)−2cos(x)sin(x)−1−sin(x)=0 a 2 cos(x)sin(x) to sin(2x)

30 paź 22:09

Mateush444: i chyba 1 trygonometryczna jest ktora mozna rozpisac

30 paź 22:10

Mateush444: dziwne cuda mi na kartce powychodzily

30 paź 22:13

Mateush444:

30 paź 22:13

ZKS: 2cos(x) − 2sin(x)cos(x) − (1 − sin(x)) = 0 2cos(x) − 2sin(x)cos(x) − 1 + sin(x) = 0 Nie zamieniaj 2sin(x)cos(x) na sin(2x) tylko popatrz się jeszcze raz na równanie i spróbuj coś zauważyć.

30 paź 22:15

Mateush444: rozwiniety wzor skroconego mnozenia raczej nie bo ten cos i sin nie jest do ²

30 paź 22:19

Mateush444: chyba ze 1 rozpisac na jedynke trygonometryczna i wtedy skroconego emotka

30 paź 22:19

Mateush444: 2cos(x) − 2sin(x)cos(x) − 1 + sin(x) = 0 2cos(x) − 2sin(x)cos(x) − cos(x)²+sin(x)² + sin(x) = 0

30 paź 22:21

Mateush444: tylko ze jest −cos(x)²...

30 paź 22:21

Mateush444: lub przerzucic na druga strone wtedy problem teoretycznie znika

30 paź 22:22

Mateush444: 2cos(x) + sin(x) = cos(x)² + 2sin(x)cos(x) + sin(x)²

30 paź 22:23

Mateush444: 2cos(x) + sin(x) = [cos(x)+sin(x)]²

30 paź 22:24

ZKS: Nic nie zamieniaj pomyśl trochę nad tym równaniem. emotka

Robiłeś to na samym początku tego tematu z wielomianem. emotka

30 paź 22:25

ZKS: 2cos(x) − 2sin(x)cos(x) − (1 − sin(x)) = 0 Teraz myśl co by tu zrobić. emotka

30 paź 22:26

Mateush444: kurna

30 paź 22:27

ZKS: Idzie czy nie idzie?

30 paź 22:29

Mateush444: parametr jakis? emotka

30 paź 22:29

Mateush444: opornie jakoś

30 paź 22:30

Mateush444: przed nawias cos wyciągnąć?

30 paź 22:31

Mateush444: np 2cos(x)

30 paź 22:31

ZKS: Tak.

30 paź 22:32

Mateush444: 2cos(X)* (1−sin(x)) − (1−sin(x)) =0

30 paź 22:33

ZKS:

jedziesz dalej. emotka

30 paź 22:33

Mateush444: wyjdzie 2cos(x) − 1?

30 paź 22:34

Mateush444: 2cos(x) = 1

30 paź 22:35

Mateush444:

	1
cos(x)=
	2

30 paź 22:35

Mateush444: czyli pi/3 + 2*k*pi i chwila drugi jeszcze tylko narysuje cosinusa sobie

30 paź 22:36

Mateush444: i tamto na minusie bo to parzysta funkcja emotka

30 paź 22:37

ZKS: Ale ten drugi nawias się obraził na Ciebie bo go po prostu olałeś i pyta się dlaczego? emotka

30 paź 22:41

Mateush444: jedno i drugie podzielilem przez (1−sin(x))

30 paź 22:42

Mateush444: czyli −1 z drugiego nawiasu emotka

30 paź 22:43

Mateush444: tzn 1 ale minus jest przed

30 paź 22:43

Mateush444: mam nadzieje ze jest dobrze

30 paź 22:44

Mateush444: mialbym jeszcze pytanie do 6 z kartki co wyslalem jak masz chwile emotka

30 paź 22:50

ZKS: Wiec otrzymałeś

	1
cos(x) =		∨ sin(x) = 1?
	2

Tak myślałem że jeszcze zapytasz o to 6.

30 paź 22:53

Mateush444: a skad tego sinusa obliczyc?

30 paź 22:55

Mateush444: w 6 to ja bym zlogarytmowal (logarytm przy podstawie z 6)

30 paź 22:55

Mateush444: moglbym gg dostac?

albo ja bym dal emotka

30 paź 22:56

Mateush444: nie bede czesto glowy zawracal tylko w kryzysowych sytuacjach

30 paź 22:57

Mateush444: wyszlo mi x = 6⁻⁴ i x = 6³

30 paź 22:59

Mateush444: no i tam zalozenie x>0

30 paź 23:00

ZKS: A obliczyłeś sin(x) = 1? emotka

30 paź 23:02

Mateush444: pi/2 + 2*k*pi? emotka

30 paź 23:03

asdf: arccos1/2 = arcsin1 =

30 paź 23:04

Mateush444: pierwiastek z 2 /2 czyli pi/4? pi/2?

30 paź 23:06

ZKS: W porządku. emotka

Zadanie szóste bym inaczej zrobił. zał. x > 0 6^log²₆x + x^log₆x = 12 6^{log₆x^log₆x} + x^log₆x = 12 x^log₆x + x^log₆x = 12 2 * x^log₆x = 12 x^log₆x = 6 (log₆x = y ⇒ x = 6^y) 6^y² = 6¹ y² = 1 ⇒ y = ±1

	1
x = 6 ∨ x =
	6

30 paź 23:06

Mateush444:

30 paź 23:07

Mateush444: czemu log²6x=log₆x^log₆x myslalem ze to log₆x * log₆x emotka

30 paź 23:09

Mateush444: ta 6 na dole

30 paź 23:10

ZKS: Jak zapewne wiesz r * log_ab = log_ab^r i stąd to się wzięło. emotka

30 paź 23:16

Mateush444: a to nie ma roznicy czy r jest przed czy po b? mi sie zdaje ze jak jest po b to samo b do potegi a przed to caly logarytm

30 paź 23:17

Mateush444: wsumie dziala jak zrobilem to na przykladzie.

30 paź 23:21

asdf: log_ab^c = c * log_ab 2log₃9 = log₃9² = log₃81 = 4 2 log₃9 = 2 * 2 = 4 rozumisz?

30 paź 23:21

ZKS: Mnożenia jest przemienne więc bez różnicy czy log_ab * r czy r * log_ab w obu przypadkach log_ab^r a poza tym masz dwa takie same wyrażenia log₆x * log₆x.

30 paź 23:22

Mateush444: juz tak

tez ogarnalem na przykladzie. tylko nie wiem czemu moim sposobem jais kosmos emotka

30 paź 23:23

Mateush444: pewnie cos powalilem...

30 paź 23:24

Mateush444: ile to log₆x^log₆x ? ja napisalem ze to log₆x

30 paź 23:26

Mateush444: chyba jednak nie tak bedzie bo tam x jest a nie 6 wiec tak sie nie zwinie....

30 paź 23:28

ZKS: a^log_ab = b My mamy: 6^{log₆x^log₆x} więc x^log₆x. Rozumiesz? emotka

30 paź 23:31

Mateush444: tak juz ogarnalem cale

jak sie tak patrzy to latwiej

najgorzej na pomysl wpasc i te wzory miec przed oczami jak sie od razu spojrzy emotka

30 paź 23:32

Mateush444: studiujesz cos z matematyka zwiazanego? emotka

30 paź 23:33

ZKS: Najlepiej to mieć wzory w głowie wtedy od razu widać nieraz rozwiązanie.

30 paź 23:33

Mateush444: a na 4 rzucisz okiem? emotka

30 paź 23:34

Mateush444: x=arcsin(x) cos(x)=pi/4 ? tak zaczynac?

30 paź 23:35

ZKS: Nie studiuję matematyki mój kierunek jest średnio związany z tym przedmiotem.

30 paź 23:35

Mateush444: czy tam α zamiast x bo juz jest

30 paź 23:36

Mateush444: no bo matme pro ogarniasz

30 paź 23:36

Mateush444: czyli z tamtego asc sin(x)= pi/4 ?

30 paź 23:37

Mateush444:

	√2
czyli x=		?
	2

30 paź 23:38

Mateush444: zapewne zle mysle

30 paź 23:38

ZKS: Tak ale nie tylko. emotka

Później pokaże inny sposób.

30 paź 23:40

Mateush444: nie tylko? emotka

30 paź 23:40

Mateush444: przeciez to ograniczona funkcja

30 paź 23:40

Mateush444: a bo tam jeszcze −pi/4

30 paź 23:41

Mateush444: czyli tamto na minusie jeszcze

30 paź 23:42

Mateush444:

	−π		π
zalozenia beda? ze x∊<		;		> czy nie trzeba?
	2		2

30 paź 23:46

ZKS: Trzeba. emotka

30 paź 23:48

Mateush444: w 3. Parametr zamiast arccos(x)=t bym wstawil

30 paź 23:49

Mateush444: a to ze na minusie to drugie dobre rozwiazanie? emotka

30 paź 23:49

ZKS:

	1
x = ±		jak to dostałeś to .
	√2

30 paź 23:51

ZKS: To ja podam inny sposób. cos(arcsin(x)) = √1 − x²

	1
√1 − x² ≤		/ ² zał x ∊ [−1 ; 1]
	√2

	1
1 − x² ≤
	2

	1
x² ≥
	2

	1		1		1		1
x ≥		∨ x ≤ −		⇒ x ∊ (−∞ ; −		] ∪ [		; ∞)
	√2		√2		√2		√2

	1		1
x ∊ (−∞ ; −		] ∪ [		; ∞) ∧ x ∊ [−1 ; 1] ⇒
	√2		√2

	1		1
x ∊ [−1 ; −		] ∪ [		; 1]
	√2		√2

30 paź 23:52

Mateush444:

	√2
czyli wyciagnac pierwiastek mianownika i wyjdzie
	2

30 paź 23:52

ZKS: Nie parametr a zmienną pomocniczą. emotka

30 paź 23:53

ZKS: Tak to jest to samo.

30 paź 23:54

Mateush444:

	1
łooo a skad √		to sie rowna pierwiastek z 1−x² 8−O
	2

30 paź 23:55

Mateush444: wez za mnie pojdz na te kolokwium

please

30 paź 23:57

ZKS: cos(arcsin(x)) = √1 − x²

30 paź 23:58

Mateush444: w przykladzie bylo 1/2 pod pierwiastkiem

30 paź 23:59

Mateush444: czy to wyniklo z jakiegos magicznego wzoru?

31 paź 00:00

Mateush444: dla rozrywki prosze http://mistrzowie.org/472204/

31 paź 00:02

ZKS: Czytałem to po południu.

Ja napisałem że cos(arcsin(x)) może zapisać inaczej tak √1 − x² wstawiając to do nierówności otrzymujemy:

	1
√1 − x² ≤		.
	√2

31 paź 00:04

Mateush444: tak nie ogarne tego przykladu

31 paź 00:05

Mateush444: 5 na przedzialach trzeba zrobic? i podstawiac no nie?

to ogarnal bym chyba

31 paź 00:06

Mateush444: 3 moduły będą i pozniej wybierac liczby z przedzialu itd

31 paź 00:08

ZKS: Tak będzie pięć przedziałów. emotka

31 paź 00:09

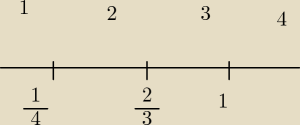
Mateush444: rysunek

a nie 4?

31 paź 00:11

Mateush444:

	1
i zalozenie x≥−
	4

31 paź 00:13

ZKS: Dobrze że czuwasz jasne że cztery. emotka

Ale do czego to założenie się odnosi?

31 paź 00:16

Mateush444: bo tam pierwiastki sa czyli liczba musi byc dodatnia

31 paź 00:17

Mateush444: czy zastosowanie modulow wyklucza juz to? bo wiadomo ze z modulu zawsze dodatnia wyjdzie

31 paź 00:20

ZKS:

	1
Czyli na przedziale x ∊ (−∞ ; −		) \|4x + 1\| = −(4x + 1) \|3x − 2\| = −(3x − 2) \|x − 1\| = −(x
	4

− 1)

	1		2
Teraz napisz jak będą wyglądały dla x ∊ [−		;		).
	4		3

31 paź 00:26

Mateush444: −3x+2−x+1=4x+1 −7x=−2

	2
x=
	7

31 paź 00:30

Mateush444: w pierwszym mi wyszlo −3x+2−x+1=−4x−1 0=−4 czyli sprzeczne

31 paź 00:31

Mateush444: a w drugim x jest poprawny bo znajduje sie w tym przedziale

31 paź 00:33

Mateush444: w 3 wychodzi taki sam x jak w drugim czyli tu nie dziala

31 paź 00:35

ZKS: To zapisz jak wygląda to równanie w drugim przedziale. emotka

31 paź 00:36

Mateush444:

	1
w czwartym niby x = −		czyli nie nalezy
	3

	2
odpowiedz dobra to x =
	7

31 paź 00:37

ZKS: Ślepy już jestem.

Nie wiem czemu ja tam widziałem wartości bezwzględne. emotka

31 paź 00:37

Mateush444:

	2
napisalem na drugi tam co wyszlo x=
	7

31 paź 00:38

ZKS: Ustal dziedzinę tego równania. emotka

31 paź 00:38

Mateush444: czyli zle wszystko

31 paź 00:38

Mateush444: nieeeeeeeee

31 paź 00:38

Mateush444: x∊<1; ∞> ?

31 paź 00:39

ZKS: Bo zacząłeś pisać o modułach to ja myślałem że to są wartości bezwzględne a to są pierwiastki po prostu.

31 paź 00:41

ZKS: Tak teraz obustronnie do kwadratu. emotka

31 paź 00:41

Mateush444: to wszedzie znikna pierwiastki czy tam zrobi sie skroconego po lewej?

31 paź 00:42

ZKS: Po lewej będziesz miał wzór skróconego mnożenia. emotka

31 paź 00:44

Mateush444: dobra dzieki wielkie za pomoc

ja ide spac bo juz mam halucyny od tego wszystkiego a musze sie wyspac do 7

jeszcze raz wielkie dzieki za pomoc emotka

do uslyszenia

31 paź 00:47

ZKS: Ale wyszedł Ci wynik? emotka

31 paź 00:50

ZKS: 3x − 2 + x − 1 + 2 * √(3x − 2)(x − 1) = 4x + 1 √(3x − 2)(x − 1) = 2 / ² 3x² − 5x + 2 = 4 3x² − 5x − 2 = 0 3x² − 6x + x − 2 = 0 3x(x − 2) + x − 2 = 0

	1
(x − 2)(3x + 1) = 0 ⇒ x = 2 ∨ x = −		∧ x ∊ [1 ; ∞) ⇒ x = 2
	3

31 paź 00:55

ZKS: Dobranoc i do następnego może. emotka

31 paź 00:56