Zbadaj monotoniczność ciągów studentpg93: Zbadaj monotoniczność ciągu: a_n= √n²+1 Z moich obliczeń na razie wyszło : a_n+1 − a_n = √n²+2n+2 −√n²+1. Według mnie ciąg jest rosnący, bo a_n+1 > a_n, ponieważ.. dodając do n jedynkę, zawsze będzie to większe od n.

aniabb: teraz góra i dół razy to samo tylko z plusem

aniabb:

	2n+1
=		>0
	√(n+1)2+1+√n2+1

studentpg93: a czy mogłabyś bardziej dokładnie? ;>

aniabb:

	a2−b2
a−b=
	a+b

studentpg93: już zrobiłem, ale przyznam się szczerze, że tego wzoru nie rozumiem...

aniabb: taki myk żeby się pierwiastków pozbyć i odejmowania bo w granicach nie można odejmować nieskończoności

	(a−b)(a+b)		a2−b2
a−b =		=
	a+b		a+b

Mila: 1) a_n>0

an+1		√(n+1)2+1
	=		>1
an		√n2+1

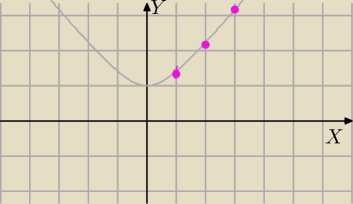
ponieważ n²+2n+2>n²+1⇔2n>−1 zatem ciąg jest rosnący 2) Można narysować wykres funkcji f(x)=√n²+1 dla argumentów dodatnich funkcja jest rosnąca, zatem dla n∊N₊też jest rosnąca

studentpg93: Aha okej, dzięki kolejny przykład:

	2n
an =
	(n+1)!

	−2n
Na razie doszedłem do tego −−> an+1 − an =		. Jeśli nie popełniłem
	(n+2)(n+1)(n−1)!

błędu, to co dalej?

aniabb: na dole nawiasy są dodatnie góra ujemna więc ułamek <0 malejący

studentpg93: a skąd wynika, że (n−1)! jest dodatni?

aniabb: bo silnia to iloczyn kolejnych liczb dla n=1 0! =1 z definicji dla n=2 1!=1 dla n=3 2!=1*2=2 itd...

studentpg93:

	(2n)!
okej, kumam. A czy mogę jakoś to skrócić? −−>
	n!

Ajtek: yyyyyy chyba nie. Ale niech aniabb sie wypowie

studentpg93:

	(2n)!
Bo mam teraz przykład: an =
	n!

	(2n+2)! − (2n)!
Na razie doszedłem do −−> an+1 − an =		, co dalej?
	(n+1)!

studentpg93: O ile się oczywiście nie pomyliłem ;>

studentpg93: hmm

Ajtek: Wg mnie to powinno wyglądać tak:

(2n+2)!		(2n)!		n!(2n+2)!−(2n)!(n+1)!
	−		=
(n+1)!		n!		n!(n+1)!

Mianownik zawsze >0, teraz nalezy rozpatrzyć znak licznika. Ja nie mam na to dzisiaj głowy.

Timmy: W tym przypadku lepiej jest policzyć iloraz.

Mila: II sposób

an+1		(2n+2)!		(2n)!		(2n+2)!		n!
	=		:		=		*		=
an		(n+1)!		n!		(n+1)!		(2n)!

	(2n)!*(2n+1)*(2n+2)		n!		(2n+1)(2n+2)
=		*		=		=2(2n+1)>1
	n!*(n+1)		(2n)!		n+1

ciąg rosnący