Prawdopodobieństwo klasyczne czołg: Test składa się z 10 pytań na ktore możemy odpowiedzieć "tak" lub "nie". Oblicz prawdopodobieństwo zaliczenia testu, jeśli odpowiedzi wskazujemy losowo oraz musimy odpowiedzieć poprawnie: a) na wszystkie pytania b)na co najmniej 9 pytań Proszę o wytłumaczenie z góry dzięki

Kejt: masz może odpowiedzi? wychodzi mi:

	1
a)
	210

czołg: w odpowiedziach jest

	1
a)
	1024

	11
b)
	1024

ale jak rozwiazac to zadanie

Kejt: czyli w a) mam dobrze masz możliwości: Tak / Nie każdą z nich wybierasz z prawdopodobieństwem 1/2 musisz trafić w 10. więc (1/2)¹0 jak nie rozumiesz to spróbuj narysować sobie drzewko. (jak nie wiesz jak to pytaj)

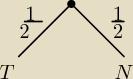
czołg: i co dalej?

Kejt: losujesz tak 10 razy, czyli drzewko powinno mieć 10 pięter.

	1		1		1
ale już chyba teraz widzisz, że będziesz przemnażał		*		*		... i tak 10 razy?
	2		2		2

czołg: czyli b bedzie podobnie tylko do 9 razy?

Kejt: nie.. mamy tutaj sporo możliwości. jedną odpowiedź możemy mieć błędną, czyli może być: TTTTTTTTTN NTTTTTTTTT TNTTTTTTTT itd.. trzeba policzyć ile tego jest na początek. oczywiście nie ręcznie, tylko trzeba pomyśleć.

Kejt: ale może też być TTTTTTTTTTT

czołg: no to będzie 11 możliwości NTTTTTTTTT TNTTTTTTTT TTNTTTTTTT TTTNTTTTTT TTTTNTTTTT TTTTTNTTTT TTTTTTNTTT TTTTTTTNTT TTTTTTTTNT TTTTTTTTTN TTTTTTTTTT

czołg: i co dalej?

Kejt: a jednak się uparł no to będzie:

	1
(		)10*11
	2

	1
prawdopodobieństwo każdego z tych przypadków wynosi (		)10
	2

a przypadków jest 11 więc..

czołg: więc do b będzie działanie

	1		11
(		)10 *11 =		i taka odpowiedź może byc?
	2		1024

Kejt: nawet masz, w odpowiedziach

czołg: tzn chcialem sie spytac czy jesli napisze tylko to do przykladu b to bedzie to wporzadku

Kejt: możesz to zawsze jakoś słownie ująć i uzasadnić swoje obliczenia..

czołg: raczej się obędzie dzięki za pomoc

Kejt: nie ma sprawy