banalne ptytanie
Saizou : | | x4−16 | |
naszkicuj wykres funkcji określonej wzorem f(x)= |
| i podaj rozwiązanie |
| | x2−4 | |
nierówności f(x) ≤8
zatem
D: x∊R\{−2:2}
| | (x2−4)(x2+4) | |
f(x)= |
| =x2+4 powstała nam funkcja kwadratowa i pytanie czy ta dziedzina |
| | x2−4 | |
którą wyznaczyłem obowiązuje dalej dla f(x)=x
2+4
29 paź 16:47
Piotr:
tak !
29 paź 16:48
Artur_z_miasta_Neptuna:
oczywiście, że obowiązuje
29 paź 16:48
Saizou : bo mi coś tu nie pasowało, ale jak teraz bym wstawił np. 2 to otrzymam 4+4=8
29 paź 16:49
Piotr:
interesuje Cie pierwotna funkcja i tam 2 i −2 wstawiac nie mozesz i nie obliczysz wartosci
funkcji !
29 paź 16:51
ZKS:
Dlatego robi się założenia najpierw żeby można było to wyrażenie uprościć.
29 paź 16:52
Mila:
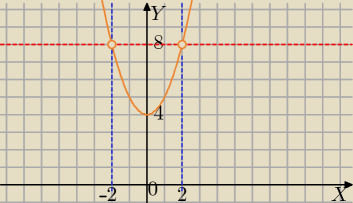
f(x)≤8⇔x∊(−2;2)
29 paź 16:56
Saizou : Mila dziękuję ale to już zrobiłem, ale dzięki za chęci. Może w weekend coś się podciągnę z
matmy więc będę tu dość często
29 paź 16:57
 f(x)≤8⇔x∊(−2;2)
f(x)≤8⇔x∊(−2;2)