Oblicz wartośc wyrażenia Matematyk: Oblicz wartośc wyrażenia:

	√2
a)arcsin		+ arcctg(−1)
	2

	1		√3
b)arcctg		+arcos(−		)
	√3		2

	8π
c)arcsin(sin
	5

	2		1
d) sin(arcsin		+arccos		)
	3		3

	3		8
e)cos(arcos		+ arcsin		)
	5		17

	2		1
f)tg (arctg		+ arccos		)
	3		3

g)arctg(2−√3) + arccos(sin ^15π₇)

	7π
h) arctg(tg		− arcctg(−1)
	8

Za wszelką pomoc będę bardzo wdzięczna i z góry dziękuje

Godzio: Ło matko, więcej niż 2 przykładów Ci nie zrobię ... Jak sam nie będzie robić to nie ma sensu studiować ...

	√2		π		π
a) arcsin		+ arcctg(−1) =		+ (−		) = 0
	2		4		4

d)

	2		2
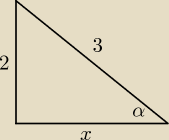
arcsin		= α ⇔ sinα =		(RYS)
	3		3

	√5
x2 + 22 = 32 ⇔ x = √5, cosα =
	3

	1		1		2√2
analogicznie: arccos		= β ⇔ cosβ =		⇒ sinβ =
	3		3		3

	2		1
Liczymy: sin(arcsin		+ arccos		) = sin(α + β) = sinαcosβ + cosαsinβ =
	3		3

	2		1		√5		2√2		2 + 2√10
=		*		+		*		=
	3		3		3		3		9

Mila:

	3		8
e) w=cos(arccos		+arcsin		)
	5		17

	3		8		3		8
arccos		=α i arcsin		=β⇔		=cosα i		=sinβ
	5		17		5		17

korzystamy z wzoru: cos(α+β)=cosα cosβ− sinα sinβ sinα i cos β oblicz z jedynki trygonometrycznej, następnie podstaw do wzoru (podobnie jak zrobił Godzio)

Matematyk: Dzieki bardzo a ktoś wie może jak zrobic podpunkt c? dopiero to zaczynam wiec proszę o wyrozumiałość

Mila:

	8π
arcsin(sin		)=
	5

	π		π
główny przedział wartości arcsinus to (−		;		)
	2		2

8π
	jest kątem IV ćwiartki
5

	8π		2π		π
sin(		)=sin(2π−		)=−sin
	5		5		5

	8π		2π		2π		2π
arcsin(sin		)=arcsin(−sin		)=−arcsin(sin		)=−
	5		5		5		5