wykres Ala: narysuj wykres funckji tg(x−π)/2 i podaj jego monotoniczność, dziedzinę itp.

Ala: bardzo potrzebuję

Mila: Funkcja

	x−π
1) tg		taki wzór?
	2

czy taki:

	π
2)tg(x−		)
	2

Saizou :

	tg(x−π)		1
czy też taki		=		tg(x−π)
	2		2

Ala: ten 1) tg^x−π₂ zupełnie nie wiem za co się zabrać, a muszę jeszcze wypisac wszystko: dziedzinę, monotoniczność, przeciwdziedzinę, okresowość itp.

Ala: rysuje wykres w programie ale nie rożni się on zbytnio od standardowego tg(x). Nie wiem tylko jak go opisać

Ala: jest mi ktoś w stanie pomóc ?

Ala: brakuje mi tylko opisu do niego

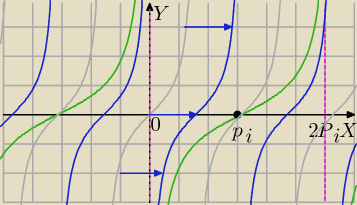
Mila: 1) wykres a)g(x)= tg(x) (popielaty)

	π
b)g(x)→T[π/2;0] h(x)=tg(x−		) niebieski
	2

rozciągniecie wykresu h(x) wzdłuż osi OX i mamy

	x		π
f(x)=tg(		−		) zielony. Okres T=2π
	2		2

Do opisu narysuję jeszcze raz tylko jeden.

Ala: super ! już go rysuję. Siedzę na tym i siedzę.. jeszcze tylko ten opis

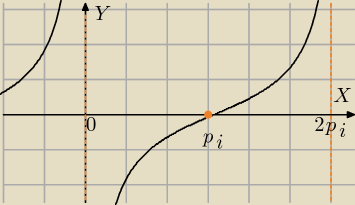
Mila: 2) dziedzina

x		π		π
	−		≠		)+kπ; k∊C
2		2		2

x
	≠π+kπ⇔x≠2π+2kπ
2

2) funkcja rosnąca w przedziałach: (2kπ;2π+2kπ) i k∊C 3) przecidziedzina =R 4) T=2π okres

Ala: a jak jest z parzystością i różnowartościową ? i czy istnieje funkcja przeciwna

Mila: Jest różnowartościowa w każdym przedziale, jak podałam wyżej i w takim przedziale ma funkcję odwrotną. Funkcja odwrotna dla przedziału: x∊(0;2π)

	x		π
y=tg(		−		) Obustronnie arctg
	2		2

	x		π		π
arctgy=		−		/+
	2		2		2

	π		x
arctgy+		=		/*2
	2		2

x=2arctgy+π Zamiana zmiennych y=2arctgx+π