nierówność wykładnicza Ania:

	x		√9
3 do potęgi		>
	x+2		1   3 do potęgi   x−1

M:

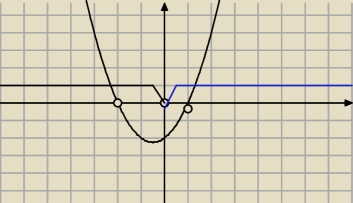
Bo_ra: x≠−2 oraz x≠1

	31
3(x/(x+2}))>3/(31/x−1)) na boku		=31−(1/x−1)=3x/x−1
	31/x−1

x		x
	>
x+2		x−1

x		x
	−		>0
x+2		x−1

x(x−1)−x(x+2)
	>0
(x+2)(x−1)

x2−x−x2−2x
	>0
(x+2)(x−1)

−3x
	>0
(x+2)(x−1)

1) (−3x>0 i (x+2)(x−1)<0) x<0 i x∊(−2,1) więc x∊(−2,0) lub 2) (−3x<0 i (x+2)(x−1)>0) x>0 i x∊(−∞ −2)U(1,∞) więc x∊(1,∞) Odp . x∊(−2,0)U(1,∞)

raba: błędy rachunkowe

Bo_ra: Tak .Mogą być bo liczyłem w pamięci Możesz wskazać gdzie te błedy są ?

raba:

	x		x−2
		>
	x+2		x−1

Bo_ra: OK.