ciąg arytmetyczny Ala : Suma pięciu początkowych wyrazów ciągu arytmetycznego, w którym

⎧	a4 + a1 = 26
⎩	a5 − a3 = 12	jest równa:

a) 18 b) 40 c) 72 d) 80 i prosiłabym o dokładne rozpisanie tego zadania, bo jest mi w takiej formie potrzebne, z góry bardzo dziękuje

	a1 + an
Wzór: Sn =		* n
	2

Piotr: a co za problem rozpisac? skorzystaj ze wzoru a_n= a₁+(n−1)r np a₄ = a₁+3r i rozwiaz uklad rownan.

Ann: a_n=a₁ +(n−1)q czyli a₁+3q+a₁=26 a₁+4q−a₁−2q=12 rozwiaz ten uklad znajdziesz a₁ i q i podstaw do tego wzoru co wypisalas

Piotr: q− przyjeto ze to iloraz w ciagu geometrycznym

Ala : ok dzięki za pomoc !

Gustlik: Ala, można bez układu równań. a₄ + a₁ = 26 a₅ − a₃ = 12 a₅ − a₃ = 2r 2r=12 /:2 r=6 a₄=a₁+3r=a₁+18 a₁+18+a₁=26 2a₁=8 /:1 a₁=4 a₅=a₁+4r=4+4*6=28

	a1+a5		4+28		32
S5=		*5=		*5=		*5=16*5=80
	2		2		2

Ala : jednak prosilabym o ulozenie mi tego rownania bo chyba zle mi wyszlo, moglibyscie?

Ann: czy q czy r to tylko oznaczenia raczej malo wazne jaka literka ,raczej liczy sie co to oznacza a nie jak przyjeto

Ala : oo dziękiii Gustlik nie odświezylam strony i nie zauwazylam ze ktos napisał, o takie mi rozwiazanie chodzilo, dzięki, dzięki, dzięki! )

Ann: rownanie masz juz ulozone w 3 poscie od gory

Gustlik:

Ala : Mam jeszcze pytanie jedno Gustlik! bo to r obliczyłeś jakby z drugiej częście układu równań? czyli zawsze można to r tak wyliczać, niestosując innej metody ?

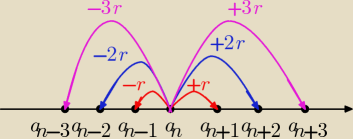Gustlik: Między dowolnymi wyrazami ciągu arytmetycznego jest tyle "r"−ów, jaka jest różnica między numerami tych wyrazów, czyli np. a₈−a₅=3r, bo 8−5=3, a₂₀−a₁₆=4r, bo 20−16=4. Na tej samej zasadzie a₅−a₃=2r, stąd 2r=12. Obrazowo: wyobraź sobie, że ciąg arytmetyczny to linia kolejowa, a kolejne wyrazy to kolejne stacje na tej linii. Jeżeli jedziesz pociągiem "do przodu", to dodajesz "r"−y, np. a₅=a₃+2r, bo ze stacji 3 do stacji 5 trzeba "podjechać" o 2 przystanki. Jeżeli jedziesz "do tyłu", np. ze stacji 9 na stację 6, to musisz się "cofnąć" o 3 przystanki, czyli a₆=a₉−3r. Jak jedziesz "do przodu" − dodajesz "r"−y, a jak się "cofasz" − odejmujesz "r"−y. Do przodu − dodajesz "r"−y, a "do tyłu" − odejmujesz "r"−y. A startuj nie z a₁, tylko z tego wyrazu, który masz podany w zadaniu. Czyli jeżeli w zadaniu masz podane, że np. a₈=12 to do innych wyrazów "jedź" z a₈, czyli ze stacji nr 8. Np. a₆=a₈−2r, a₁₂=a₈+4r itd. Ten wyraz a₈ t Twój "punkt zaczepienia". Metodę "podjeżdżania−cofania" przedstawiłem na rysunku.