Pewien ostrosłup ma 70 wierzchołków... kostka: zad. 1 Pewien ostrosłup ma 70 wierzchołków. Ile wynosi liczba jego krawędzi? zad.2 Tworząca stożka o długości 12 tworzy z jego wysokością kąt 30 stopni. Ile wynosi pole powierzchni całkowitej tego stożka? Proszę o i dziękuję za wszelką pomoc.

kostka: zadanie 2 wiem jak policzyc. Zadanie pierwsze nie kumam. A może mi ktoś pomóc jeszcze przy takim zad ? Z wycinka kołowego o powierzchni 72 pi i promieniu 12 zwinięto powierzchnie boczną stożka.Ile wynosi jego objętość? Bardzo proszę o pomoc.

Buuu: Ad. 1 Dowolny ostrosłup ma wszystkie wierzchołki przy podstawie, oprócz jednego "na czubku". Krawędzi natomiast ma 2 razy tyle co wierzchołków przy podstawie.

pigor: ... np. tak: niech w − liczba wierzchołków ostrosłupa, to w=n+1 ⇒ n= w−1= 70−1=69 wierzchołków podstawy, tyle samo krawędzi bocznych i tyle samo krawędzi podstawy, więc k=2n=2*69=138− szukana liczba krawędzi ostrosłupa .

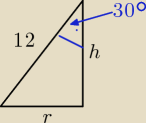
Ann: l=12 sin(30)=r/12 => r=12*sin(30) cos(30)=h/12 => h=12*cos(30) P_b=πrl P_p=πr² P_c=πr(r+l) podstawiasz i masz wynik

pigor: ... Z wycinka kołowego o powierzchni 72π i promieniu 12 zwinięto powierzchnie boczną stożka. Ile wynosi jego objętość ? otóż z warunków zadania dł. tworzącej stożka l=12 i πrl=72π /:π ⇒ 12r=72 ⇒ r=6 − dł. promienia podstawy stożka , więc dł. wysokości stożka H=√ l²−r²=√12²−6²=√6*18= 6√3 , zatem V_s= ¹₃π r²H= ¹₃π*6²*6√3= 72√3 π − szukana objętość danego stożka.

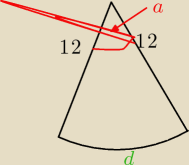
Ann: P_w=72π

	a
Pw=π*122 *
	360

72=12*12*a/360 a=6*30=180 d=2πr*180/360=π*12 d=2πr' r'=6 P_p=π(r')²=π*36 l²=h²+(r')² h²=12²−6²=6*18 h=6√3 V=P_p *h /3 i podstaw do tego wzoru