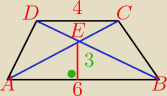
?? Kwasim: CZworokąt ABCD na rysunku jest trapezem. Oblicz pola trojkatow ABE, DEC,AED,BCE

Wiktor: abe = 9 , dec = 4 a dale nie wiem

Kwasim: ale jak to obliczyc... wyniki to sobie wiesz...

viola: wyskość trójkąta DCE oznaczam przez h. Z podobieństwa trójkatów ABE i DCE obliczam h ⁶₃=⁴_h czyli h=2 pola trójkatów ABE i DCE obliczysz z podstawowego wzoru

viola: wysokość trapezu =6 i tyle samo wynosi wysokość trójkątow CDA i CDB Oblicz ich pola

viola: przepraszam wysokość trapezu wynosi 5

Jakub: P_ABE = ¹₂*6*3 = 9 Trójkąt DEC jest podobny do trójkąty ABE więc mogę policzyć wysokość trójkąta DEC wychodzącą z wierzchołka E i padającą na podstawę DC z proporcji

3		h
	=		/*4
6		4

h = ³₆*4 h = 2 Cała wysokość trapezu ma więc h=2+3=5 P_DEC = ¹₂*4*2 = 4 P_ABD = ¹₂*6*5 = 15 P_AED = P_ABD − P_ABE = 15 − 9 = 6 P_ABC = ¹₂*6*5 = 15 P_EBC = P_ABC − P_ABE = 15 − 9 = 6 Odp. 9, 4, 6, 6

Bogdan:

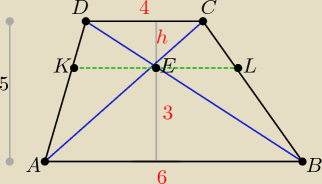
	6		4
Z podobieństwa trójkątów ABE i CED otrzymujemy:		=		⇒ h = 2
	4		h

Pole trójkata ABE: P₁ = 9 Pole trójkata CED: P₂ = 4.

	4		5		12
Z podobieństwa trójkątów ACD i AEK otrzymujemy:		=		⇒ |KE| =
	|KE|		3		5

	4		5		12
Z podobieństwa trójkątów BCD i BEL otrzymujemy:		=		⇒ |LE| =
	|LE|		3		5

	12
|KE| = |LE| =
	5

Łatwo teraz obliczyć pola trójkątów: AEK, KED, BEL, ELC. Warto tu przytoczyć następująca zależność: Pole trójkąta AED = Pole trójkata BEC = P₃ P₃ = √P₁ * P₂ W tym zadaniu P₃ = √9 * 4 = 6