Wykresy funkcji matema: Naszkicuj wykresy poniższych funkcji i na ich podstawie określ podstawowe własności funkcji (dziedzinę, przeciwdziedzinę, miejsca przecięcia z osiami, przedziały monotoniczności, ekstrema lokalne): a) f(x)=−x²+5 b) f(x)=2−√x

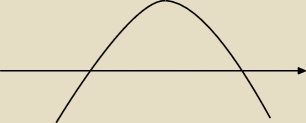
matema: widzę, że nikt nie odpisuje, więc może przedstawię moje trudy liczenia podpunktu a) −x²+5=f(x) Δ=20 √Δ=√20 Proszę o sprawdzenie obliczeń. Teraz nie wiem jak z √20 wyciągnąć te miejsca przecięcia się paraboli z osią x i w ogóle nie wiem jak dalej liczyć.

matema:

matema: pomoże ktoś

aniabb: √20=2√5

aniabb: x1=−√5 x2=√5

aniabb: dziedzina x∊R przeciwdziedzina y∊(−∞;5>

matema: x1 i x2 z wzoru na p i q

matema: ok. z delty

aniabb: z p i q to maximum

matema: D=R, wzory na p i q do przeciwdziedziny potrzebne tak

matema: co to są ekstrema lokalne jak je wyliczyć ?

matema:

matema: już wiem, że to max i min. Proszę jednak o wyliczenie podpunktu b) w miarę możliwości

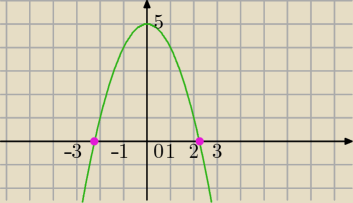
Mila: 1) f(x)=−x²+5 a) D=R x_w=0; y_w=5 współrzędnie wierzchołka paraboli Zbiór wartości funkcji Z_w=(−∞;5> b)miejsca zerowe −x²+5=0⇔x²=5⇔x=√5 lub x=−√5 Punkty przecięcia z osią OX: (√5;0) i (−√5;0) z osiąOY: (0;5) c)f(x)↑dla x∊(−∞;0) f(x) ↓ dla x∊<0;∞) d) wartość największa dla x=0 i wynosi y_max=5

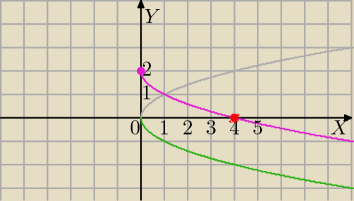
Mila: 2) f(x)=2−√x D=R₊ a) wykres: g(x)=√x szary wykres (sporządzasz częściową tabelkę wartości(0;0)(1;1)(4;2)itd) odbijasz symetrycznie względem osi OX wykres g(x) i otrzymasz wykres: h(x)=−√x (zielony) Przesuwasz wykres h(x) o 2 jednostki w górę i masz wykres : f(x)=2−√x (różowy wykres) b) miejsce zerowe 2−√x=0⇔p(x)=2 ⇔=4 Resztę opisz sam.

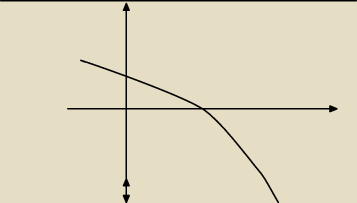
matema: trochę inny mi ten wykres wyszedł. Nie wiem czy prawidłowy. Trochę ten rysunek nie estetyczny, bo to dopiero mój początek rysowania w tym programie.

matema: y= 2 dla x=0 i minusowych x nie przyjmuje, tak mi wyszło, trochę za daleko narysowałem

matema: Proszę o sprawdzenie b) D=(0;∞) przeciw D=(2;−∞) oś Y y=2 oś X x=4 funkcja malejąca dla x∊(o;∞) ekstrema y_max = 2 dla x=0

Mila: b) 1) D=<0,∞) (Ja też zapomniałam o zerze w poprzednim poście) 2) Z_w=(−∞;2> 3) Miejsce zerowe x=4 punkty przecięcia z osiami: OY − (0;2) OX − (4;0) 4) monotoniczność f(x) f(x) malejąca dla x∊D 5) ekstrema y_max=2 dla x=0 Zaraz napiszę jaki narysowałeś wykres.

Daria: f(x)=2−√x

Daria: f(x)=3+lnx