nierówność adaś: Rozwiąż nierówność: |x|+√x²−2x+1≤2−x √x²−2x+1= √(x−1)² = |x−1| |x|+|x−1|≤2−x |x|+|x−1|+x−2≤0 1⁰ x+x−1+x−2≤0 3x≤3 x≤1 dla x≥0 2⁰ −x−x+1+x−2≤0 −x≤1 x≥−1 dla x<0 3⁰ −x+x−1+x−2≤0 x≤3 dla x<0 i x≥0 , sprzeczność 4⁰ x−x+1+x−2≤0 x≤1 dla x≥0 i x<0 ,sprzeczność. i teraz będzie przedział ? x∊<−1,1>

aniabb: te dziedziny do 3 i 4 masz skopane

aniabb: ale wynik ok http://www.wolframalpha.com/input/?i=%7Cx%7C%2B%7Cx%E2%88%921%7C%E2%89%A42%E2%88%92x+

adaś: nie rozumiem ,chodzi Tobie o przypadek 3 i 4 ? Według mnie dobrze obliczyłem nie widzę błędu

aniabb: 3° x<0 i x≥1 4° x≥0 i x<1

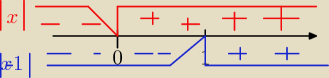
aniabb: 1° x<0 2° 0≤ x <1 3° x≥1 takie powinieneś mieć przypadki

aniabb: na rysunku najlepiej się je rozpisuje i widać

adaś: rzeczywiście ,zapomniałem o |x−1|,dzięki

aniabb: na rysunku nie będziesz niepotrzebnie sprawdzał przedziału z założenia pustego

adaś: w pierwszym przypadki także powinienem dopisać x≥0 i x≥1, tak samo w drugim x<0 i x≥1

adaś: w pierwszym przypadku*

adaś: chociaż to jest sprzeczne bo nie ma jednocześnie takie liczby

aniabb: tak

aniabb: w 2 oba mniejsze

adaś: racja dziękuje raz jeszcze